Две окружности пересекаются в точках K и L. Прямые k и l проходящие через K и L соответственно вторично пересекоют первую окружность в точках A и B, а вторую в точках C и D. Докажите что AB//CD
Ответы
Ответ дал:
0
Четырёхугольники АВLK и CDLK вписанные, значит суммы противолежащих углов в них равны 180°.
Пусть ∠BLK=α, ∠DLK=β. α=180-β и β=180-α.
В четырёхугольнике АВLK ∠КАВ=180-∠BLK=180-α=β.
В четырёхугольнике CDLK ∠KCD=180-∠DLK=180-β=α.
∠KAB+∠KCD=β+α=180°, значит они односторонние при параллельных АВ и CD и секущей АС.
АВ║CD.
Доказано.
Пусть ∠BLK=α, ∠DLK=β. α=180-β и β=180-α.
В четырёхугольнике АВLK ∠КАВ=180-∠BLK=180-α=β.
В четырёхугольнике CDLK ∠KCD=180-∠DLK=180-β=α.
∠KAB+∠KCD=β+α=180°, значит они односторонние при параллельных АВ и CD и секущей АС.
АВ║CD.
Доказано.
Приложения:
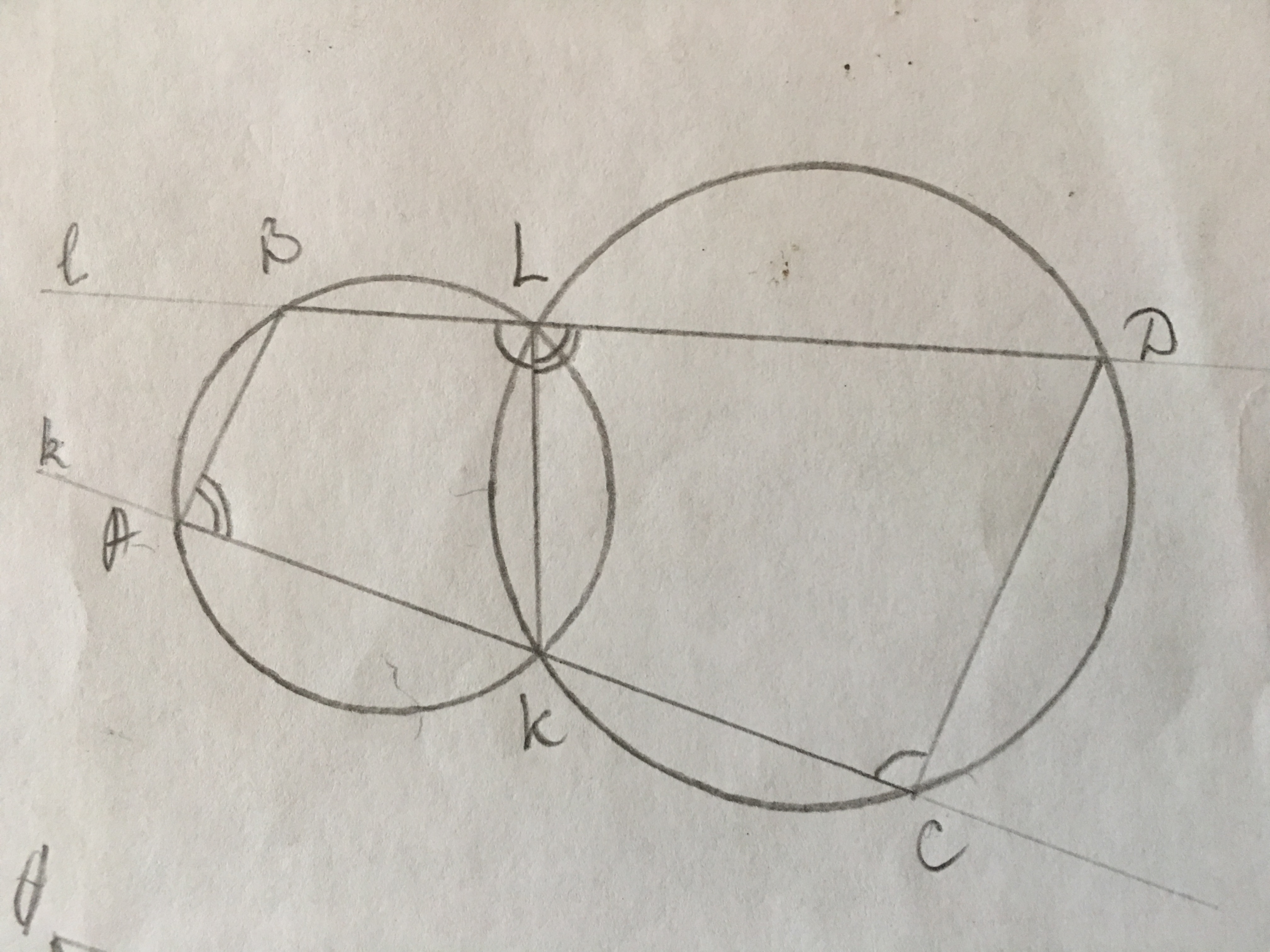
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад