Ответы
Ответ дал:
0
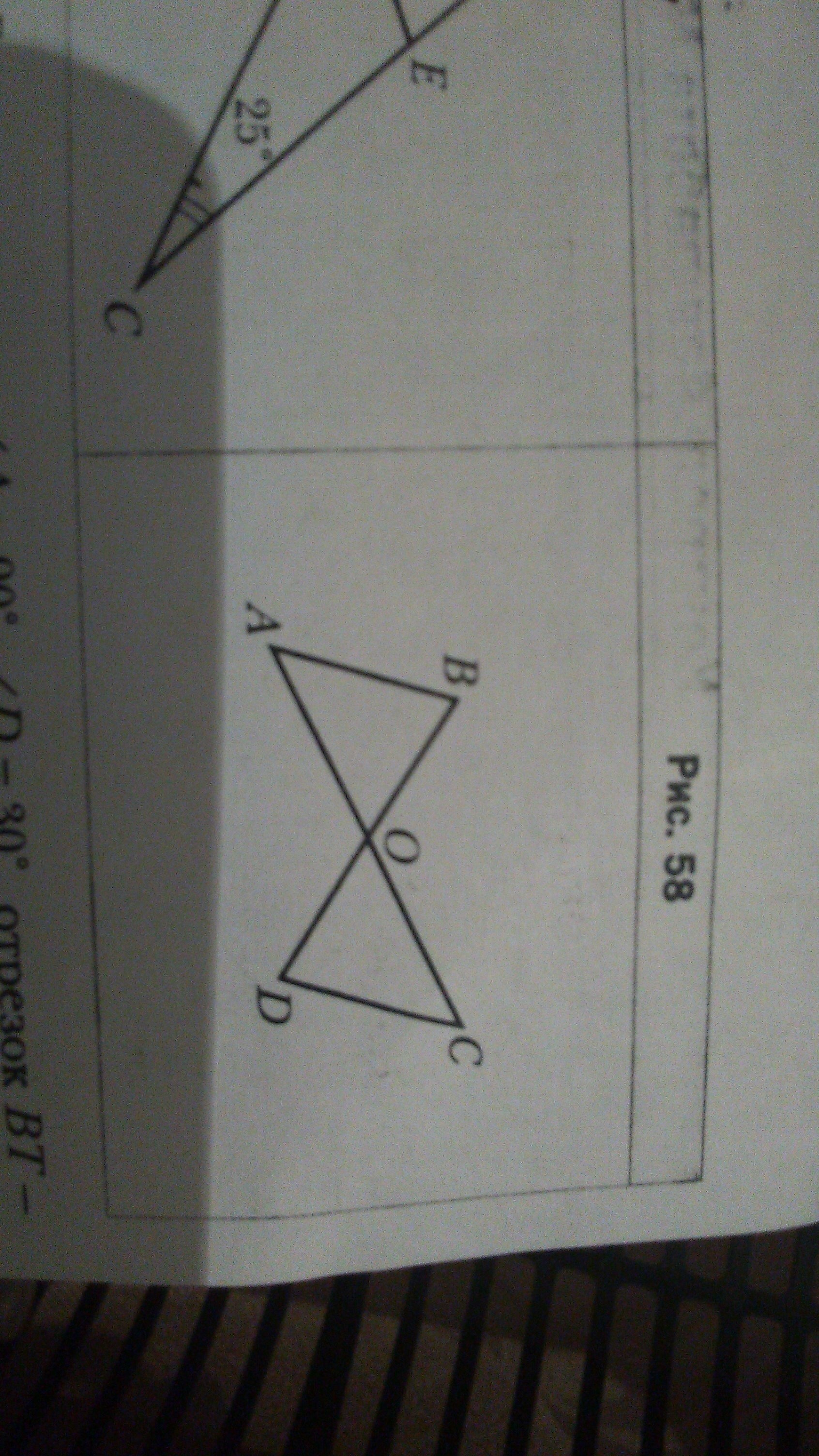
Докажите что АО = СО, если известно, что АВ = СD и АВ || CD
1) Сначала докажем равество тругольников AOB и COD
1. ∠ОАВ = ∠ ОСD как внутренние разносторонние при АВ || CD и секущей AC
2. ∠ОВA = ∠ ОDС как внутренние разносторонние при АВ || CD и секущей BD
3. AB=BC из условия
Значит, Δ AOB и Δ COD равны за одной стороной и двумя приглеглыми углами.
Значит, АО = ОС как соотвествующие стороны равных треугольников.
Доказано
Приложения:
Ответ дал:
0
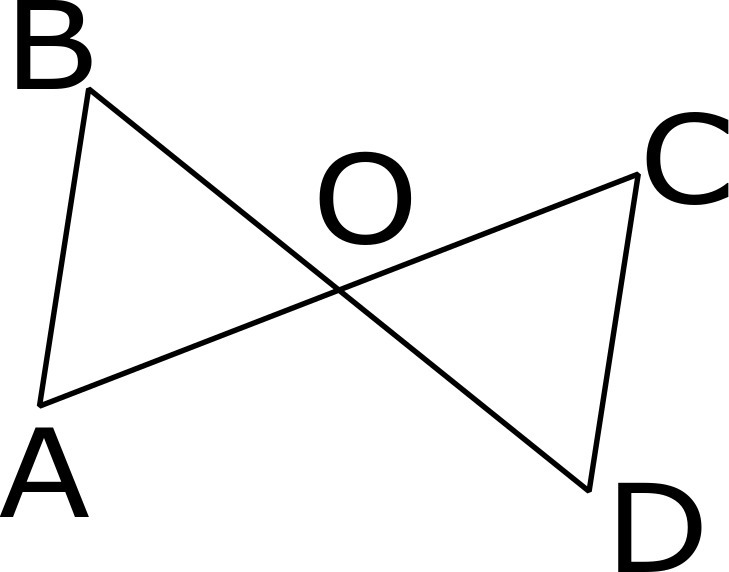
∠BAC = ∠ACD и ∠DBA = ∠BDC как накрест лежащие при AB || CD , секущей AC и BD соответственно.
Из условия AB = CD, значит ΔABO = ΔDOC по одной стороне и двум прилежащим углам.
У равных треугольников соответственные элементы(углы, стороны..) равны, т.е. AO = OC
Что и требовалось доказать.
Приложения:

Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад