Question

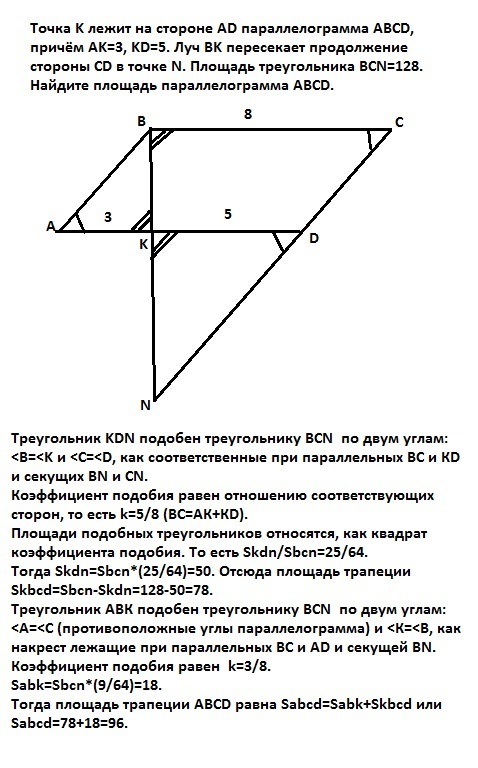
Точка K лежит на стороне AD параллелограмма ABCD, причём AK=3, KD=5. Луч BK пересекает продолжение стороны CD в точке N. Площадь треугольника BCN=128. Найдите площадь параллелограмма ABCD.
Если не трудно, прикрепите решение, спасибо!!!

Answer 1

Треугольник KDN подобен треугольнику BCN  по двум углам: <B=<K и <C=<D, как соответственные при параллельных ВС и КD и секущих ВN и СN.
Коэффициент подобия равен отношению соответствующих сторон, то есть k=5/8 (ВС=АК+КD).
Площади подобных треугольников относятся, как квадрат коэффициента подобия. То есть Skdn/Sbcn=25/64.
Тогда Skdn=Sbcn*(25/64)=50. Отсюда площадь трапеции Skbcd=Sbcn-Skdn=128-50=78.
Треугольник АВК подобен треугольнику BCN  по двум углам: <А=<С (противоположные углы параллелограмма) и <К=<В, как накрест лежащие при параллельных ВС и АD и секущей ВN. Коэффициент подобия равен  k=3/8.
Sabk=Sbcn*(9/64)=18.
Тогда площадь трапеции АВСD равна Sabcd=Sabk+Skbcd или
Sabcd=78+18=96.  Это ответ.