Ответы
Ответ дал:
0
Ответ: 4335
Объяснение:
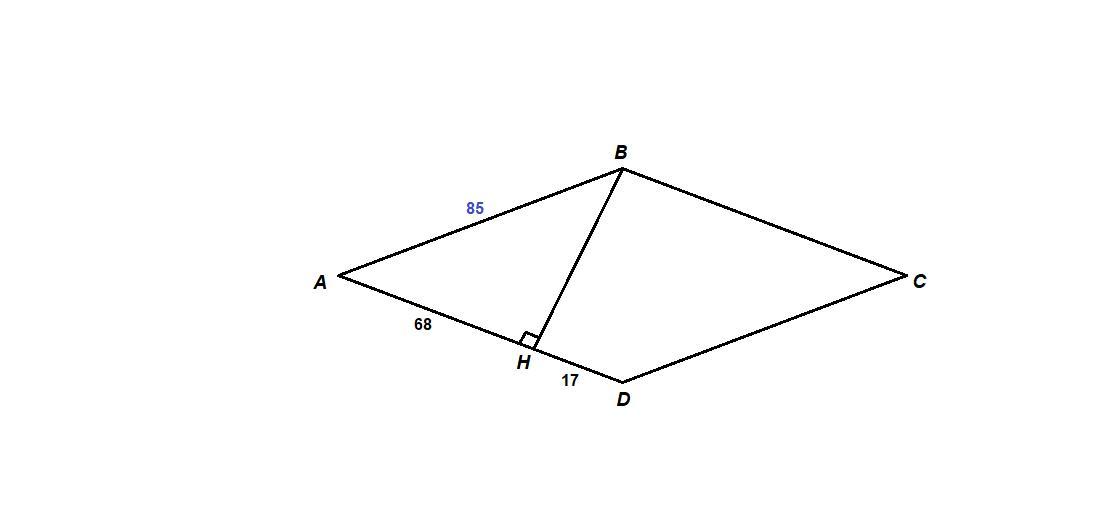
AD = AH + HD = 68 + 17 = 85
Стороны ромба равны, поэтому
AB = AD = 85
ΔABH: ∠AHB = 90°, по теореме Пифагора
Площадь ромба можно найти как произведение стороны на проведенную к ней высоту:
Sabcd = AD · BH
Sabcd = 85 · 51 = 4335 кв. ед.
Приложения:
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад