Question

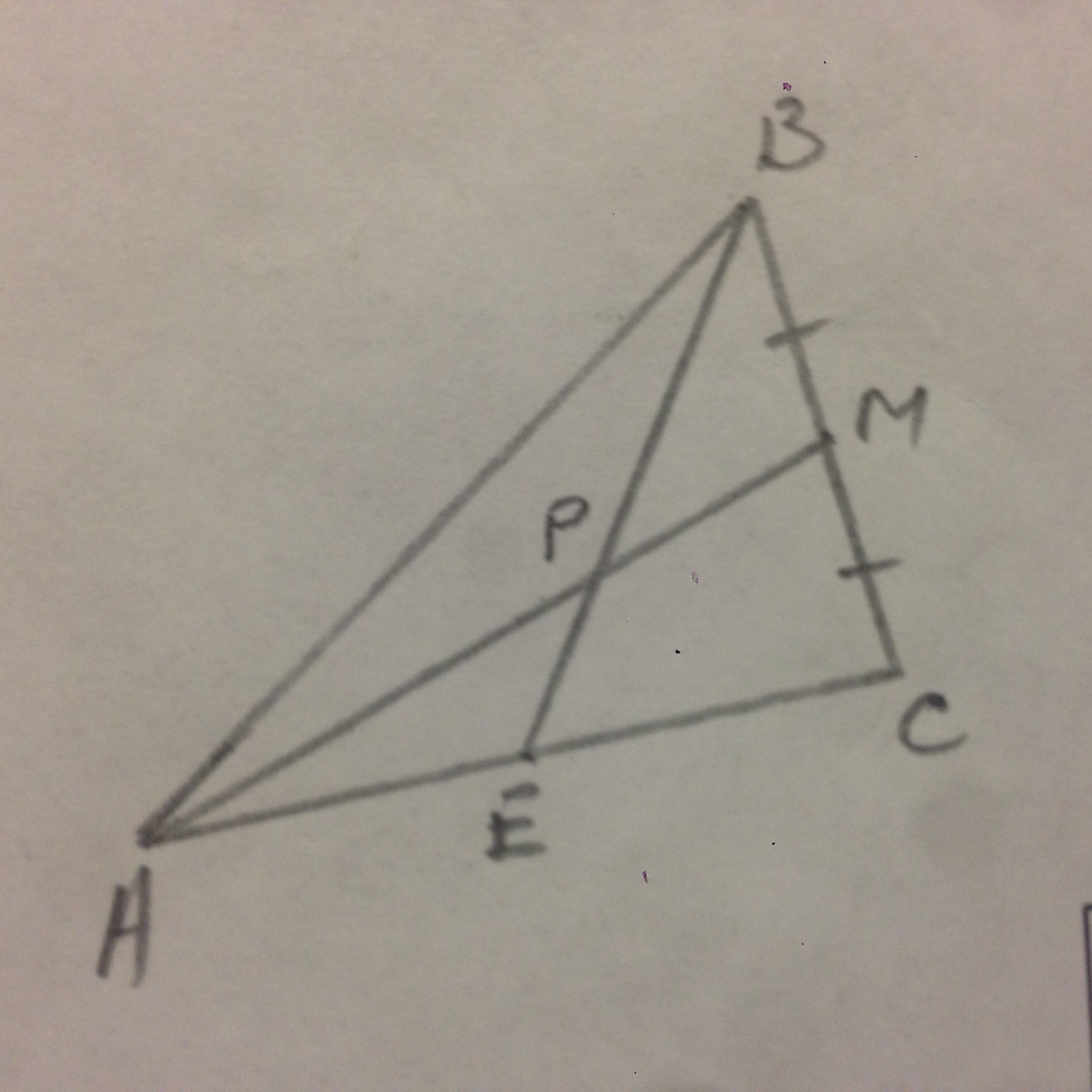
На стороне АС треугольника АВС взята точка Е так, что АЕ:ЕС=3:4. В каком отношении медиана АМ: 1)делит отрезок ВЕ. 2)делится отрезком ВЕ?

Answer 1

АМ ∩ ВЕ = Р.
АЕ:ЕС=3:4 ⇒ АЕ:АС=3:7.

1) Применим теорему Менелая для треугольника ЕВС и наклонной АМ:
(СМ/МВ)·(ВР/РЕ)·(АЕ/АС)=1,
(1/1)·(ВР/РЕ)·(3/7)=1,
ВР/РЕ=7/3.

2)Применим ту же теорему для тр-ка АМС и наклонной ЕВ:
(СЕ/АЕ)·(АР/РМ)·(ВМ/ВС)=1,
(4/3)·(АР/РМ)·(1/2)=1,
АР/РМ=6/4=3/2.

Ответ: ВР:РЕ=7:3, АР:РМ=3:2.