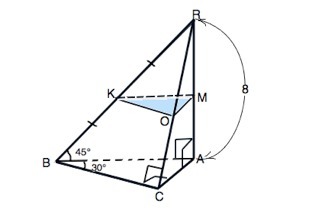
Основание пирамиды RABC- треугольник Abc,в котором угол с=90,а угол В=30 градусов. Ребро AR перпендикулярно к плоскости основания пирамиды и равно 8,а ребро BR образует с плоскостью основания угол 45. Через середину ребра BR проведена плоскость параллельно плоскости основания пирамиды. Найдите площадь боковой поверхности пирамиды, отсеченной этой плоскостью
Ответы
Ответ дал:
0
Плоскость МКО, параллельная плоскости ∆ АВС, пересекает боковые грани по прямым, параллельным сторонам основания АВС и отсекает от исходной пирамиды подобную ей пирамиду RMKO.
Площади подобных фигур относятся как квадрат отношения их линейных размеров.
k=RK:RВ=1/2 ⇒ k²=1/4
Площадь боковой поверхности пирамиды RABC равна сумме площадей её боковых граней.
S ∆ RAB=RA•AB/2
AB=RA•ctg45°=8
S ∆ RAB=8•8/2=32
S ∆ RAC=RA•AC/2
AC=AB•sin30°=8·1/2=4
S ∆ RAC=4·8/2= 16
S ∆ RCB=RC·BC/2
BC=AB·cos30•=4√3
RC по т.Пифагора=√(AC²+AR²)=√(16≠64)=4√5
S ∆ RCB=(4√5)·(4√3)/2=8√15
S бок RABC=32+16+8√15=8·(6+√15)
S бок RMKO= S бок RABC:4=2·(6+√15) ед. площади.
Приложения:
Вас заинтересует
2 года назад
9 лет назад
9 лет назад
10 лет назад