Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 60 градусам и 135, а CD=24
Ответы
Ответ дал:
0
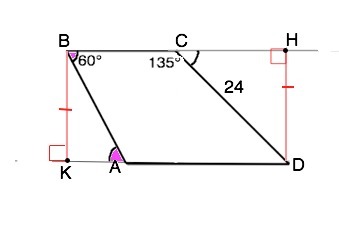
Продлим основания трапеции и проведем к их продолжениям перпендикуляр DH, и перпендикуляр ВК.
В ∆ СНD - угол НСD смежный углу 135° и равен 45°. Тогда угол СDН=45°. ⇒DH=CD•sin 45°=24•√2/2=12√2
ВК=DH=12√2
∠ВАК=∠АВС=60° - накрестлежащие.
АВ=ВК:sin60°=12√2):(√3/2)=8√6
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад