Question

Докажите, что в прямоугольной треугольника медианы, проведенная из вершины прямого угла, равна половине гипотенузы
7 КЛАСС

Answer 1

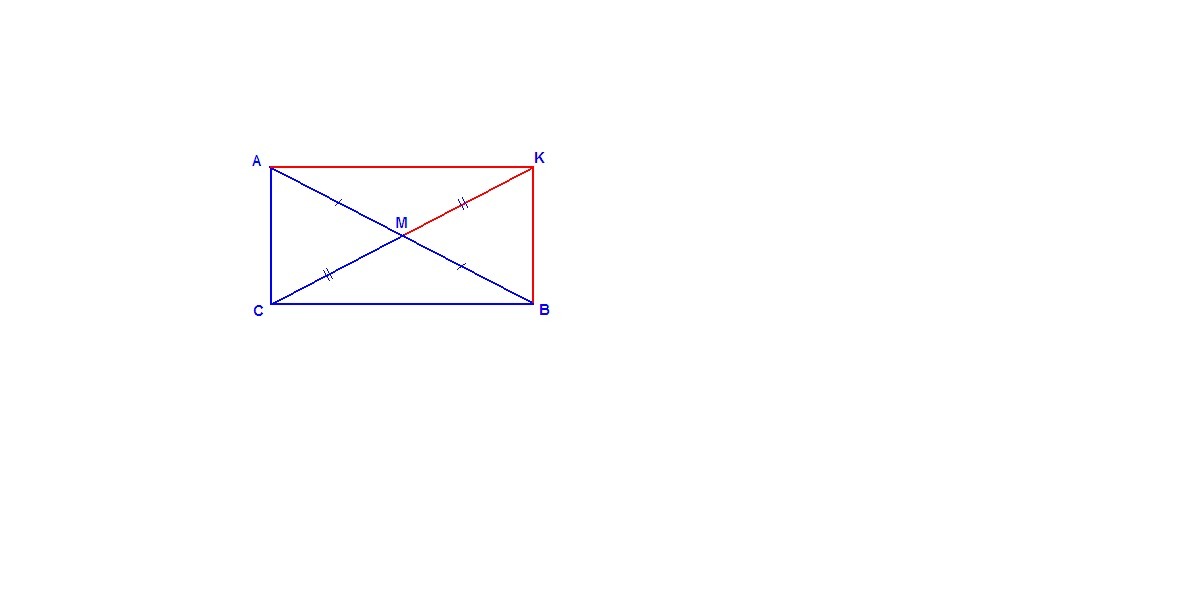
В ΔАВС ∠С = 90°, СМ - медиана, проведенная к гипотенузе.

Продлим медиану за точку М и отложим отрезок МК = СМ.

В четырехугольнике АСВК диагонали точкой пересечения делятся пополам, значит это параллелограмм по признаку параллелограмма.

Уол АСВ равен 90°, значит АСВК - прямоугольник.

Диагонали прямоугольника равны, поэтому

СМ = АМ = МВ, т.е. СМ = 1/2 АВ.

значит медиана, проведенная к гипотенузе, равна ее половине.