Постройте график функции y=|1-(x+3)^2| и определите, при каких значениях "с" прямая y=c имеет с графиком ровно две общие точки.
Ответы
Ответ дал:
0
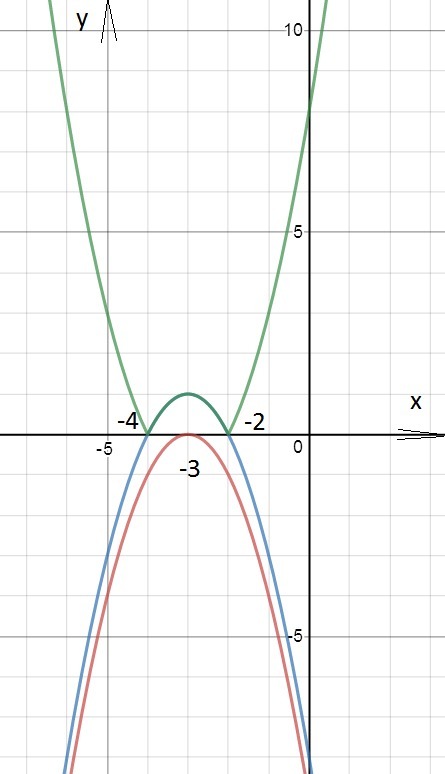
Строим параболу у=-(х+3)² (красного цвета)
Вершина в точке х=-3; у=0
ветви вниз.
Строим параболу у=1-(х+3)² ( синего цвета), все ординаты которой на 1 больше чем ординаты параболы у=-(х+3)²
Часть графика у=1-(х+3)², расположенную ниже оси Ох, отражаем симметрично оси Ох. Получаем кривую зеленого цвета.
Прямая у=0 и прямые у=с при с>1 имеет с графиком ровно две общие точки.
О т в е т. с=0 и с>1
Вершина в точке х=-3; у=0
ветви вниз.
Строим параболу у=1-(х+3)² ( синего цвета), все ординаты которой на 1 больше чем ординаты параболы у=-(х+3)²
Часть графика у=1-(х+3)², расположенную ниже оси Ох, отражаем симметрично оси Ох. Получаем кривую зеленого цвета.
Прямая у=0 и прямые у=с при с>1 имеет с графиком ровно две общие точки.
О т в е т. с=0 и с>1
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
10 лет назад