Question

диаметр основания конуса равен 48, а длина образующей -25. найдите площадь осевого сечения этого конуса

Answer 1

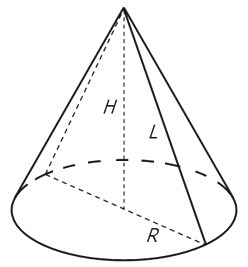
Пусть образующая это L, высота это H, радиус основания это R. 

Радиус основания равен половине диаметра, то есть 24.

Вычислим высоту и далее используя формулу площади треугольника найдём искомую площадь. По теореме Пифагора:

H = √(L^2 - R^2) = √(25^2 - 24^2) = √49 = 7

Вычисляем площадь сечения:

S = 1/2*D*H = 1/2*48*7 = 168 ед. кв

Ответ
168