Question

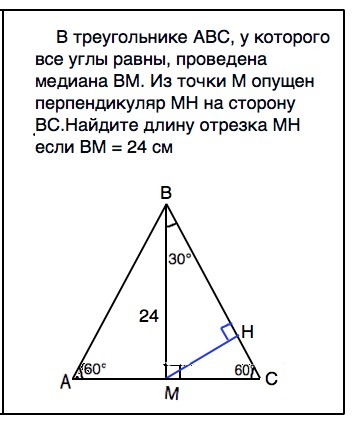
В треугольнике ABC, у которого все углы равны, проведена медиана BM. Из точки М опущен перпендикуляр MH на сторону BC. Найдите длину отрезка MH, если BM = 24 см.
Помогите пожалуйста!

Answer 1

Так как углы ∆ АВС равны, каждый из них равен 60°, а сам треугольник - правильный.

Перпендикуляр ВМ - высота, медиана и биссектриса ∆ АВС.

∆ ВМС - прямоугольный. В ∆ ВМН   МН перпендикулярен ВС,  он  противолежит углу МВН,  равному 30° ( т.к. ВМ - биссектриса). ⇒ 

МН  равен половине гипотенузы ВМ . 

МН=ВМ:2=12 см