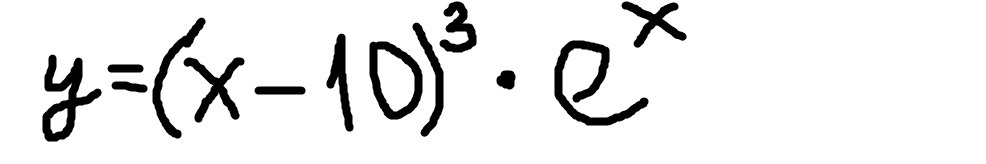Question

Помогите пожалуйста! Найти точку минимума функции

Answer 1

1. Найти производную, 3*(x-10)²*eˣ + (x-10)³*eˣ=eˣ*(x-10)²*(x-7)
2. Приравнять её к нулю и наути корень уравнения: x=10; 7.
3. Выяснить при помощи метода интервалов, какие промежутки (а их три: от -∞ до 7, от 7 до 10 и от 10 до +∞) положительны, а какие отрицательны.
4. Так как (-∞;7) отрицательный, а (7;10) - положительный, то х=7 - точки минимума, в которой значение функции равно у= -3³*е⁷= -27е⁷

Answer 2

У меня сначала 7-как точка максимума, а со второй попытки- минимума. Теперь понятно, спасибо)

Answer 3

В арифметике, похоже, была "неполадка". Успеха!