Question

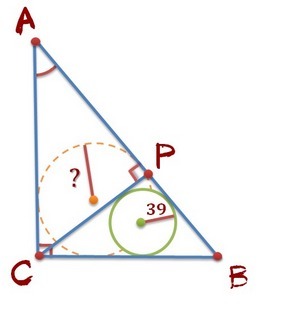
Из вершины прямого угла C треугольника ABC проведена высота CP. Радиус окружности, вписанной в треугольник BCP, равен 39, тангенс угла BAC равен 3/4. Найдите радиус окружности, вписанной в треугольник ABC.

Answer 1

Решение.Треугольник ВРС подобен треугольнику АРС. Так как тангес угла это отношение катета, противолежащему к данному углу, ко второму катету. tg∠А=ВС/AC=3/4. Если принять АС=4х, ВС =3х. то по теореме Пифагора АВ =5х. Теперь мы можем сказать что так как треуг. подобны, то коэф подобия будет 3/5.
Следовательно и радиусы вписан окружностей имеют тот же коэф подобия R=39· 5/3=65

Answer 2

Неверно :(

Answer 3

спасибо большое