В прямоугольной трапеции основания равны 8 см и 10 см, а один из углов равен 〖45〗^° . Найдите площадь трапеции.
Ответы
Ответ дал:
0
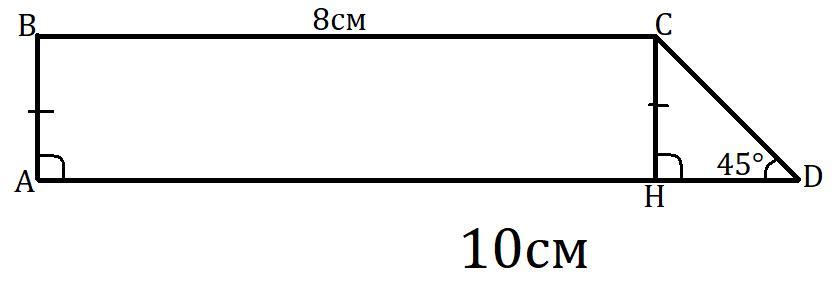
Дана трапеция ABCD, BC║AD. BC=8см, AD=10см.
Найти S(ABCD).
Пусть CH⊥AD и H∈AD. Тогда ABCH - прямоугольник. AH=BC=8см.
HD = AD-AH = 10-8 = 2 см
В прямоугольном ΔCHD (∠H=90°): ∠CDH=45° ⇒ ∠DCH=90°-45°=45° ⇒ ΔCHD - равнобедренный CH=HD=2см.
Высота трапеции равна произведению высоты и средней линии.
S(ABCD) = CH·(BC+AD)/2 = 2·(8+10)/2 = 8+10 = 18 см²
Ответ: 18см².
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад