Ответы
Ответ дал:
0
ABCD - правильный тетраэдр, значит, все ребра равны
AB = BC = AC = AD = BD = CD = 12
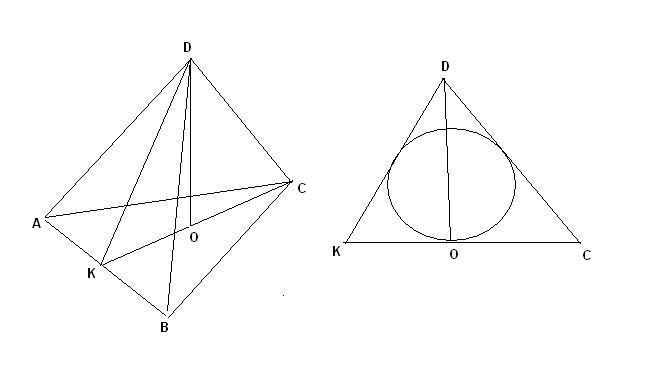
Проведем сечение плоскостью через ребро CD и через K середину AB.
Тогда шар, вписанный в куб в плоскости станет кругом, вписанным в треугольник. Это показано на правом рисунке.
CK = DK = 12*√3/2 = 6√3
Найдем площадь треугольника CDK по формуле Герона.
p = (a+b+c)/2 = (12+6√3+6√3)/2 = 6+6√3


Радиус вписанного круга (он же радиус шара)

Площадь поверхности вписанного шара

AB = BC = AC = AD = BD = CD = 12
Проведем сечение плоскостью через ребро CD и через K середину AB.
Тогда шар, вписанный в куб в плоскости станет кругом, вписанным в треугольник. Это показано на правом рисунке.
CK = DK = 12*√3/2 = 6√3
Найдем площадь треугольника CDK по формуле Герона.
p = (a+b+c)/2 = (12+6√3+6√3)/2 = 6+6√3
Радиус вписанного круга (он же радиус шара)
Площадь поверхности вписанного шара
Приложения:
Вас заинтересует
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
