Question

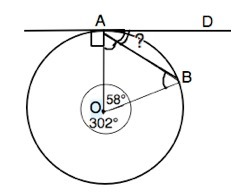
Две точки окружности делят окружность на две равные 58° и 302°.
Найдите велечину угла DAB между касательной к окружности и хордой.

Answer 1

Теорема:     Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами

Угол DAB=58:2=29°. 

Как это найдено. 

Радиусы, проведенные в точку касания А и в точку В,  образуют равнобедренный треугольник АОВ с углами при АВ, равными (180°-58°):2=61°

Угол ОАD=90°, угол BAD=90°-61°=29°