Ответы
Ответ дал:
0
Площадь фигуры ограниченной двумя функциями вычисляется по формуле:
границы интегрирования заданны в условии.
Получаем:
Ответ:
Ответ дал:
0
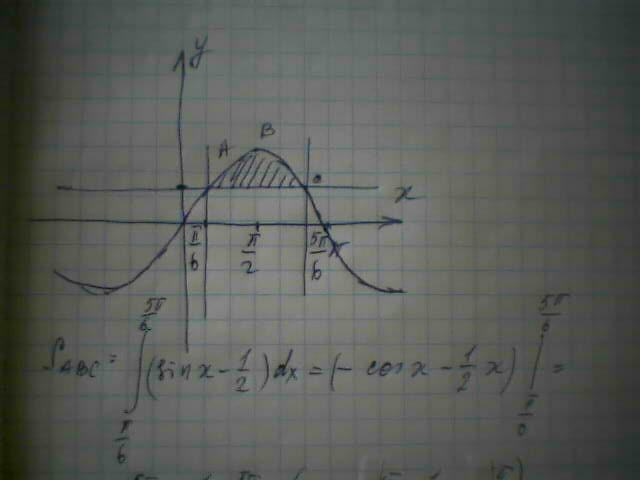
Решение Вашего задания во вложении
Приложения:

Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад