В прямоугольлном треугольнике с катетами 36 и48 на гипотенузе взята точка. из нее проведены прямые, паралленльные катетам. получился прямоугольник, вписаный в данный треугольник. где на гипотенузе надо взять точку, чтобы площадь такого прямоугольника была наибольшей?
Ответы
Ответ дал:
0
обозначим как во вложении стороны треугольника как а и b
из подобия треугольников запишем
b/36=(48-a)/48
b=36-36a/48=36-0.75a
площадь s=ab
s=36a-0.75a^2
s'=36-1.5a
s'=0 a=36/1.5=24
при а<24 производная больше нуля, функция возрастает
при а больше 24 убывает
в точке а=24 достигает максимума.
Значит искомая точка имеет координаты
а=24 b=36-.75*24=18
Приложения:
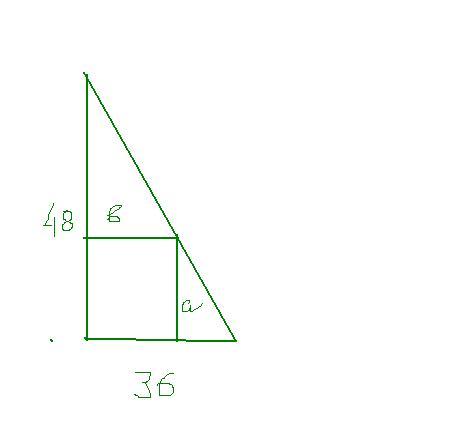
Вас заинтересует
2 года назад
2 года назад
8 лет назад
10 лет назад
10 лет назад
11 лет назад