Помогите решить данное неравенство.. Вопрос возник , вот например, (log2(2x))^2 тоже самое что и log2^2(2x)?
Приложения:
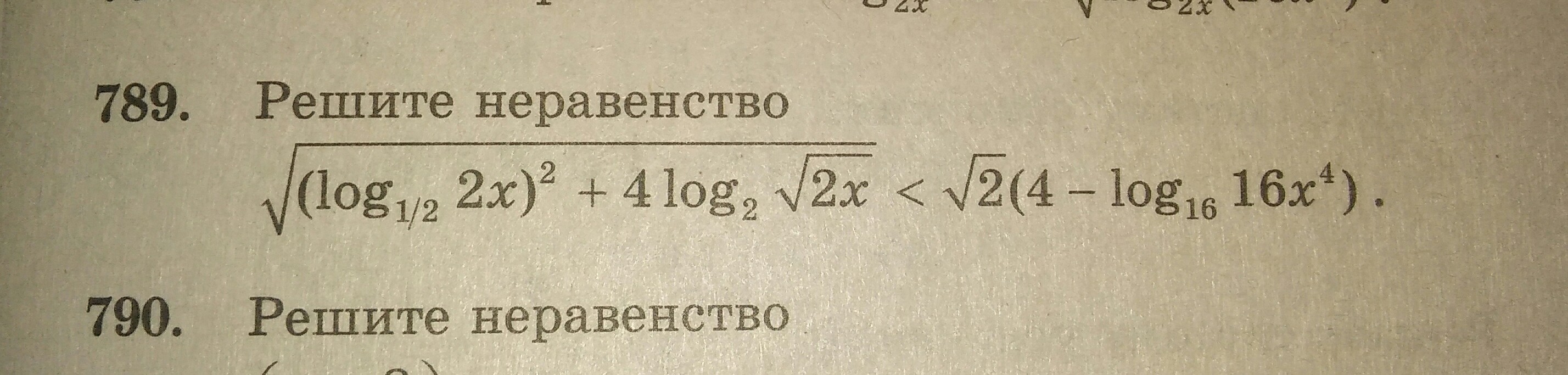
Ответы
Ответ дал:
0
(0)//////////////////////////>x
///////[1/8]....[1/2]/////>x
Рассматриваем равносильную систему:
1)///////////////////////////[1/8] [1/2]////////////////////////////////////////>x
2) (-8)////////(0)//////////////////////////////////(8) >x
3)//////////////////////////////////////////////////////(2) (32768)//////>x
ОД3: (0)//[1/8] [1/2]////////////////////////////////////////>x
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад