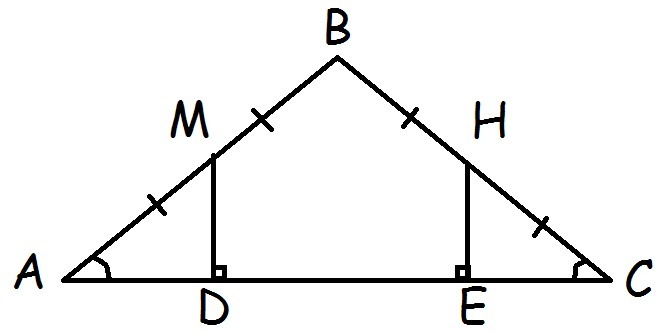
в треугольнике ABC AD равно BC. Точки М и Н середины сторон, АВ и ВС. MD и HE перпендикулярна к прямой AC. Докажите что треугольник, АМD равен треугольнику, СНЕ.( можно рисунок)
Ответы
Ответ дал:
0
ЕСЛИ AB=BC, ТО ТРЕУГОЛЬНИК РАВНОБЕДРЕННЫЙ.ИЗ ЭТОГО СЛЕДУЕТ, ЧТО УГЛЫ ПРИ ОСНОВАНИИ РАВНЫ.МН СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА И ДЕЛИТ БОКОВЫЕ СТОРОНЫ ПОПАЛАМ.MD=HE,СЛЕДОВАТЕЛЬНО AD=CE.ТАКИМ ОБРАЗОМ AMD=CHE.
Ответ дал:
0
Если АВ = ВС, то треугольник АВС равнобедренный. Тогда угол ВСА = углу ВАС.
Если АВ = ВС, а точки М и Н - середины этих сторон, то АМ = МВ = СН = ВН.
Если MD и HE перпендикулярны к прямой AC, то тругольники МDА и НЕС - прямоугольные.
У треугольников МDА и НЕС:
1) Угол ВСА = углу ВАС
2) АМ = НС
За гипотенузой и катетом треугольник АМD = треугольнику СНЕ.
Если АВ = ВС, а точки М и Н - середины этих сторон, то АМ = МВ = СН = ВН.
Если MD и HE перпендикулярны к прямой AC, то тругольники МDА и НЕС - прямоугольные.
У треугольников МDА и НЕС:
1) Угол ВСА = углу ВАС
2) АМ = НС
За гипотенузой и катетом треугольник АМD = треугольнику СНЕ.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад
10 лет назад