Question

СРОЧНО!!!
На разных гранях двугранного угла выбраны точки, удаленные от ребра угла на 20 и 30 см. Одна из точек удалена от противолежащей грани на 15 см. Найдите расстояние от второй точки до противолежащей грани.

Answer 1

пусть точка А находится на плоскости α и удалена от плоскости β на h1=20,а точка В находится на плоскости β и удалена от плоскости α на h2=30
sinФ=h1/d1=h2/d2⇒20/d1=30/15⇒d2=15*20/30=10

Answer 2

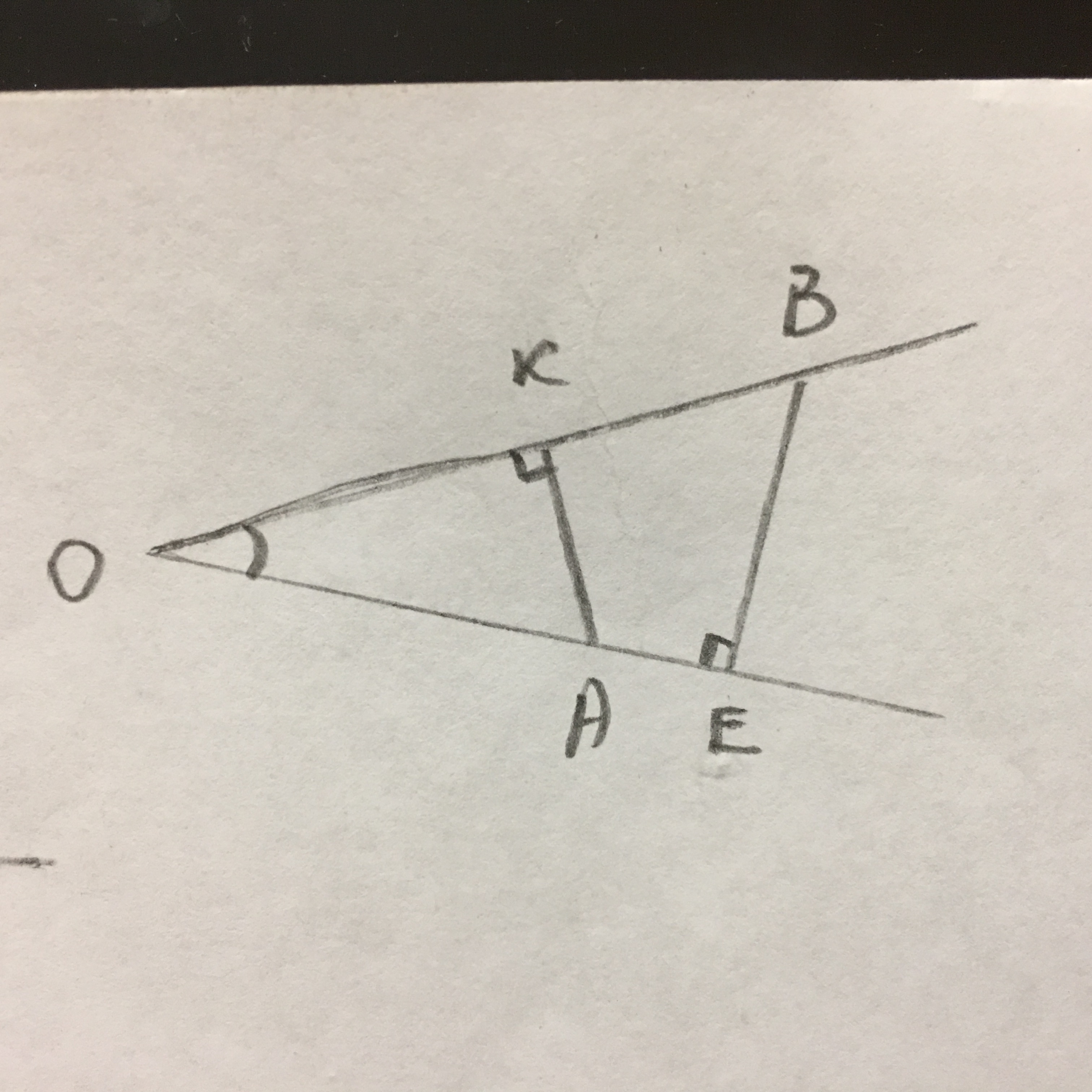
∠О - двугранный угол. АО=20 см, ВО=30 см.
КО и ЕО - проекции отрезков АО и ВО на соответствующие плоскости.
Треугольники АКО и ВЕО подобны т.к. оба прямоугольные и ∠О общий, значит АО/АК=ВО/ВЕ.
Пусть АК=15 см, тогда 20/15=30/ВЕ ⇒ ВЕ=30·15/20=22.5 см.
Пусть ВЕ=15 см, тогда 20/АК=30/15 ⇒ АК=20·15/30=10 см.
Ответ: 10 см или 22.5 см