помогите пожалуйста
решите методом интервала неравенство
дайте пожалуйста развёрнутое решение
Приложения:
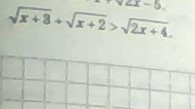
Ответы
Ответ дал:
0
Решение:
√x+3+√x+2>√2x+4. Найдем ОДЗ: {x+3≥0
{x+2≥0
{2x+4≥0, отсюда x≥-2.
Обе части неравенства неотрицательны. Возведя обе части в квадрат
получим x+3+x+2+2√(x+3)(x+2)>2x+4,
упростив получаем 2√(x+3)(x+2)>-1,это будет возможным при условии
(x+3)(x+2)≥0,_+___-3__-__-2____+_____, получаем x≤-3 или x≥-2.
учиты вая ОДЗ x≥-2, получаем ответ x≥-2.
√x+3+√x+2>√2x+4. Найдем ОДЗ: {x+3≥0
{x+2≥0
{2x+4≥0, отсюда x≥-2.
Обе части неравенства неотрицательны. Возведя обе части в квадрат
получим x+3+x+2+2√(x+3)(x+2)>2x+4,
упростив получаем 2√(x+3)(x+2)>-1,это будет возможным при условии
(x+3)(x+2)≥0,_+___-3__-__-2____+_____, получаем x≤-3 или x≥-2.
учиты вая ОДЗ x≥-2, получаем ответ x≥-2.
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
10 лет назад