Решить неравенство с модулем:
|x|-2|x-1|+4|x-3|<5x
Приложения:
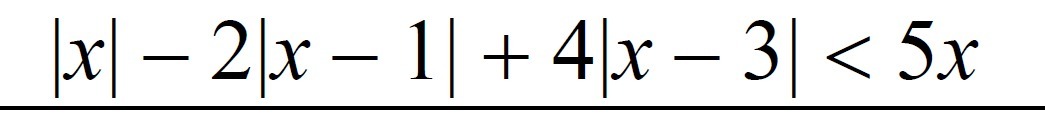
Мариарти1:
если не подошло решение не баньте пожалуйста, не хочу статус терять., ну а если что мы так решали…))
Ответы
Ответ дал:
1
|x|-2*|x-1|+4*|x-3|<5x
Подмодульные выражения равны нулю при:
x=0 x=1=0 x=1 x-3=0 x=3
-∞__________0__________1___________3___________+∞
x∈(-∞;0)
-x-2*(-x+1)+4*(-x+3)<5x
-x+2x-2-4x+12<5x
8x>10
x>1,25∉
x∈(0;1])
x-2(-x+1)+4*(-x+3)<5x
x+2x-2-4x+12<5x
7x>10
x>1³/₇∉
x∈(1;3)
x-2*(x-1)+4*(-x+3)<5x
x-2x+2-4x+12<5x
10x>14
x>1,4 ⇒ x∈(1,4;3)
x∈[3;+∞)
x-2*(x-1)+4*(x-12)<5x
x-2x+2+4x-12<5x
2x>-10
x>-5 ⇒ x∈[3;+∞)
Ответ: x∈(1,4;+∞).
Подмодульные выражения равны нулю при:
x=0 x=1=0 x=1 x-3=0 x=3
-∞__________0__________1___________3___________+∞
x∈(-∞;0)
-x-2*(-x+1)+4*(-x+3)<5x
-x+2x-2-4x+12<5x
8x>10
x>1,25∉
x∈(0;1])
x-2(-x+1)+4*(-x+3)<5x
x+2x-2-4x+12<5x
7x>10
x>1³/₇∉
x∈(1;3)
x-2*(x-1)+4*(-x+3)<5x
x-2x+2-4x+12<5x
10x>14
x>1,4 ⇒ x∈(1,4;3)
x∈[3;+∞)
x-2*(x-1)+4*(x-12)<5x
x-2x+2+4x-12<5x
2x>-10
x>-5 ⇒ x∈[3;+∞)
Ответ: x∈(1,4;+∞).
Вас заинтересует
1 год назад
1 год назад
2 года назад
2 года назад
3 года назад
3 года назад
9 лет назад