Question

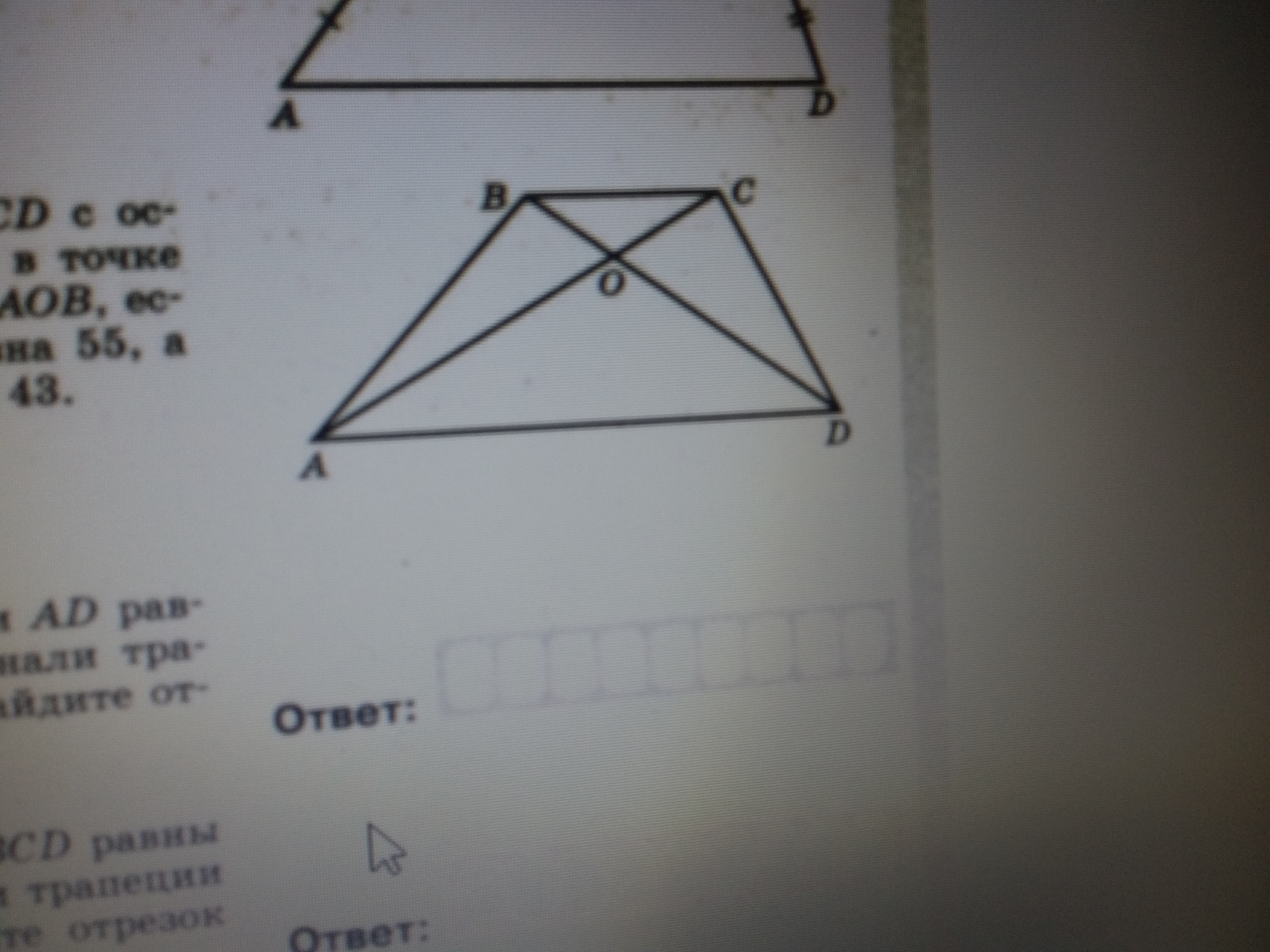
В диагонали АС и BD трапеции ABCD с основаниями BC и AD пересекаются в точке О. Найдите площадь треугольника AOB, если площадь треугольника ACD равна 55, а площадь треугольника AOD равна 43.

Answer 1

несложно доказывается, что площади треугольников АОВ и DOC равны.
для любой трапеции это известный факт:
площади треугольников, опирающихся на боковые стороны трапеции, равны.
S(AOB) = S(COD) = S(CAD) - S(OAD) = 55 - 43 = 12