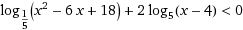Question

И снова решите неравенство.

Answer 1

log_1/5(x^2-6x+18) +2log_5(x-4)<0
-log_5(x^2-6x+18)+log_5(x-4)^2 <0
log_5(x-4)^2/(x^2-6x+18)<log_5(1)
(x-4)^2/(x^2-6x+18)<1
Так как x^2-6x+18 всегда больше нуля для всех х на числовой оси,
то умножим обе части уравнения на (x^2-6x+18)
x^2-8x+16<x^2-6x+16
  2x>0
    x>0
ОДЗ  (x-4)^2/(x^2-6x+18)>0  для всех х на числовой оси
Поэтому решением неравенства будет значения
х принадлежищие (0;+бесконечн)

Answer 2

log_1/5 (x^2 - 6x + 18)  +  2log_5(x  -  4)< 0

ОДЗ   x^2  - 6x + 18 > 0    x^2  -  6x  +  18  =  0  D  =  b^2 - 4ac  =  36 - 72 = -36<0  x  -  любое

           x  -  4  > 0  ------->   x>4

  ОДЗ      x > 4

log_5(x^2 - 6x + 18)/log_5 (1/5)  +  log_5(x - 4)^2  <  log_5 1     log_5(1/5)  =  -1

log_5(x - 4)^2  -  log_5(x^2 - 6x + 18)   <  log_5 1

log_5((x - 4)^2 / (x^2 -6x +18))   <   log_5 1

Так  как  основание  логарифма   5>1,   то  меньшему  значению  функции  соответствует

меньшее  значение  аргумента.

(x - 4)^2 / (x^2 - 6x + 18) < 1

(x - 4)^2  < x^2 -6x +18

x^2 - 8x + 16 - x^2 + 6x - 18 < 0

  -  2x  -   2  <  0  

2х  >  -2

x  >  -1

 

Ответ.   Учитывая    ОДЗ    ( 4;   +бесконечности)