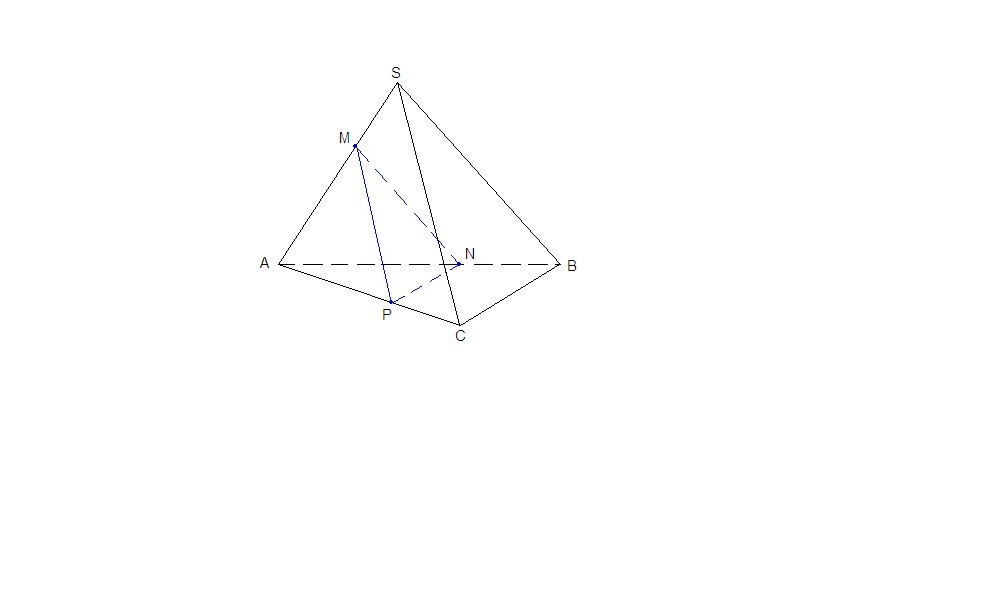
Объем пирамиды SABC равен 54. На ребрах SA, АВ и АС взяты точки М, N и Р соответственно так, что SM:MA=BN:NA=CP:PA=1:2. Найдите объем пирамиды МАNP.
Ответы
Ответ дал:
0
Если SM : MA = BN : NA = CP : PA = 1 : 2, то
АМ : АS = AN : AB = AP : AC = 2 : 3.
Пирамиды ASBC и AMNP имеют общую вершину А, одинаковые плоские углы при вершине А и равные отношения боковых ребер.
Значит пирамиды ASBC и AMNP подобны, коэффициент подобия:
k = 3/2.
Площади подобных фигур относятся как квадрат коэффициента подобия, а объёмы - как куб коэффициента подобия:
Vasbc : Vamnp = k³
Vasbc : Vamnp = 27 : 8
54 : Vamnp = 27 : 8
Vamnp = 54 · 8 / 27 = 16
АМ : АS = AN : AB = AP : AC = 2 : 3.
Пирамиды ASBC и AMNP имеют общую вершину А, одинаковые плоские углы при вершине А и равные отношения боковых ребер.
Значит пирамиды ASBC и AMNP подобны, коэффициент подобия:
k = 3/2.
Площади подобных фигур относятся как квадрат коэффициента подобия, а объёмы - как куб коэффициента подобия:
Vasbc : Vamnp = k³
Vasbc : Vamnp = 27 : 8
54 : Vamnp = 27 : 8
Vamnp = 54 · 8 / 27 = 16
Приложения:
Вас заинтересует
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад