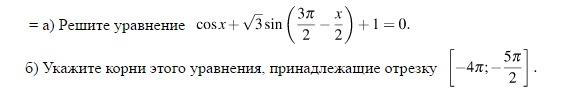Question

Ребят, очень нужно! помогите пожалуйста

Answer 1

1. Решение уравнения сводится к приведению такового к квадратному путём применения формулы приведения для синуса: cosx-√3cos(x/2)+1=0
Затем, применяя формулу двойного аргумента для косинуса, получим: 2cos²(x/2)-√3cos(x/2)=0 ⇒ cos(x/2)*(2cos(x/2)-√3)=0, откуда получаем два уравнения: cos(x/2)=0 и 2cos(x/2)-√3=0. Решения соответственно будут: x=π+2πn и x=+-π/3+4πn
2. Из первого решения в указанном отрезке содержится -3π (n= -2), а из второго -11π/3 (n= -1)

Answer 2

Вопрос : А как вы получили из 2cos(x/2)-√3=0, ответ x=+-π/3+4πn ?

Answer 3

Огромное спасибо!

Answer 4

Успеха!