Ответы
Ответ дал:
0
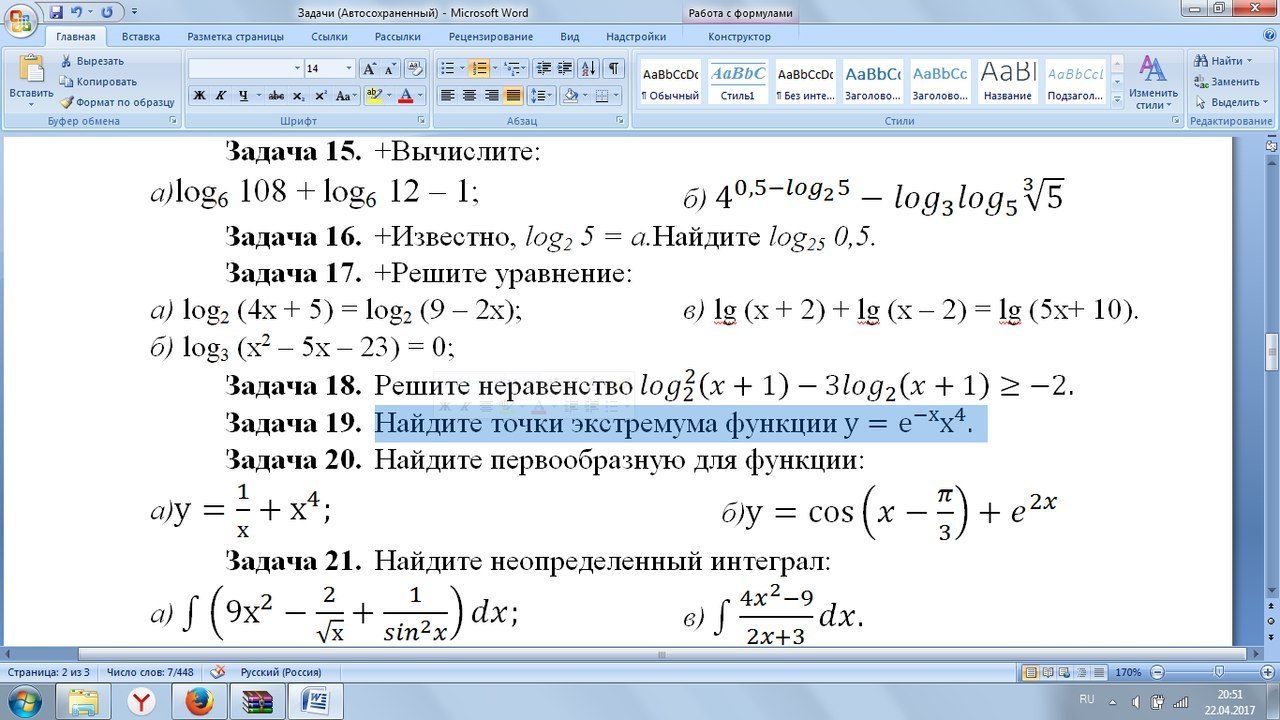
y = e⁻ˣx⁴
y' = -e⁻ˣx⁴ + e⁻ˣ·4x³ = e⁻ˣ·x³(4 - x)
Точки экстремума находим из условия: y' = 0.
x₁ = 0, x₂ = 4
y' < 0, x ∈ (-∞; 0) и y' > 0, x ∈ (0; 4) ⇒ x = 0 -- точка минимума
y' > 0, x ∈ (0; 4) и y' < 0, x ∈ (4; +∞) ⇒ x = 4 -- точка максимума
y' = -e⁻ˣx⁴ + e⁻ˣ·4x³ = e⁻ˣ·x³(4 - x)
Точки экстремума находим из условия: y' = 0.
x₁ = 0, x₂ = 4
y' < 0, x ∈ (-∞; 0) и y' > 0, x ∈ (0; 4) ⇒ x = 0 -- точка минимума
y' > 0, x ∈ (0; 4) и y' < 0, x ∈ (4; +∞) ⇒ x = 4 -- точка максимума
Вас заинтересует
2 года назад
2 года назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад