Медиана ВМ треугольника АВС является диаметром окружности, пересекающей сторону ВС в её середине. Найдите длину стороны АС, если радиус описанной около треугольника АВС окружности равен 7.
Ответы
Ответ дал:
0
так как по условию  , а угол опирающийся на диаметр прямой то есть угол
, а угол опирающийся на диаметр прямой то есть угол  , сторона
, сторона  общая для треугольников
общая для треугольников  , значит гипотенузы выше сказанных треугольников
, значит гипотенузы выше сказанных треугольников  равны, соответственно получаем равнобедренный треугольник так как
равны, соответственно получаем равнобедренный треугольник так как  , отсюда следует что гипотенузы- это радиусы
, отсюда следует что гипотенузы- это радиусы  , а значит
, а значит 
Приложения:
Ответ дал:
0
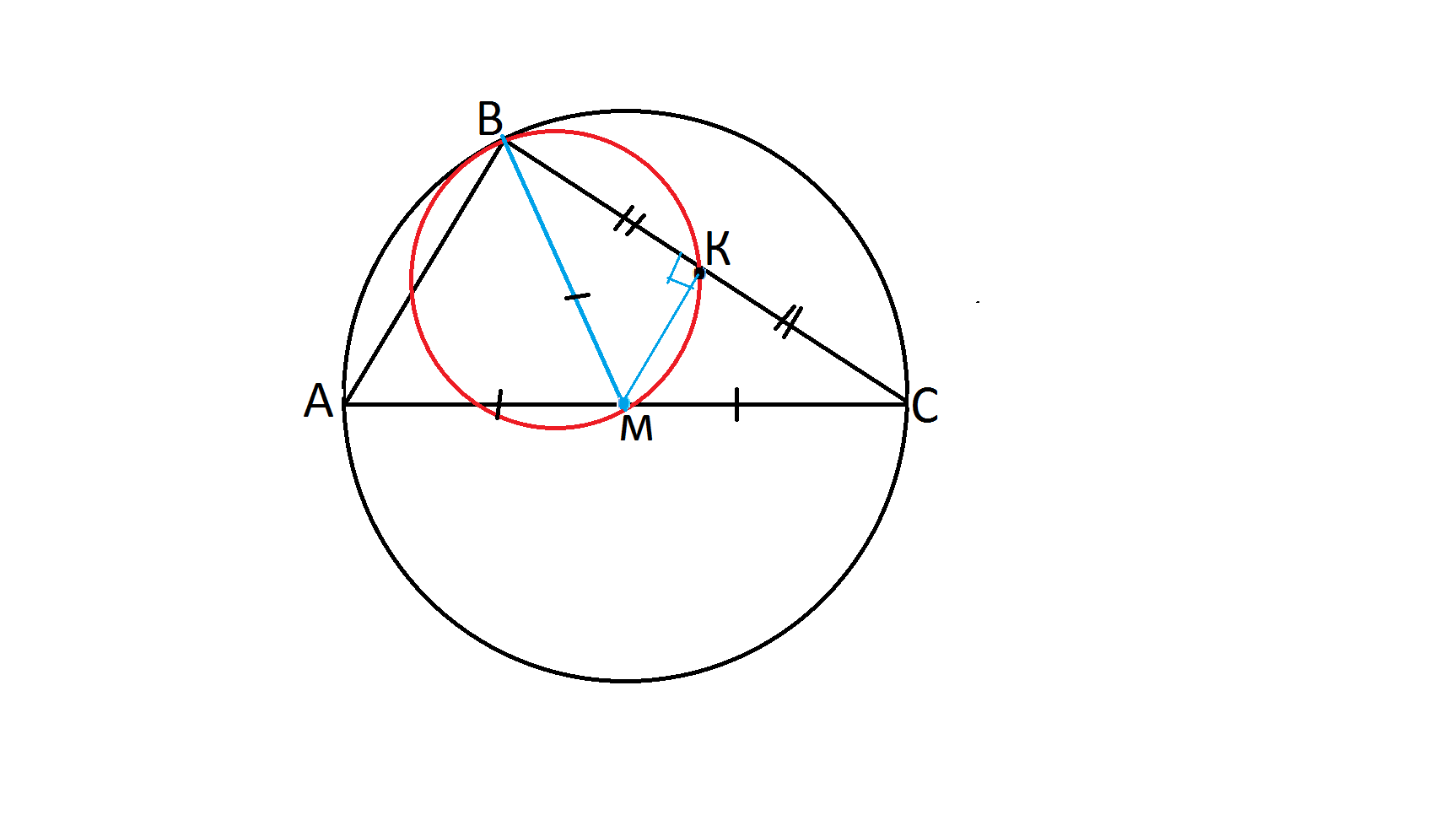
Сделаем рисунок и рассмотрим треугольник ВМС.
По условию ВК=КС,
МК - медиана треугольника ВМС.
Так как ВМ - диаметр описанной вокруг треугольника ВМК окружности, - треугольник ВКМ прямоугольный.
Тогда КМ - высота треугольника ВМС, но она же и медиана.
Треугольник, в котором высота является медианой - равнобедренный.
Треугольник ВМС - равнобедренный.
ВМ=МС.
Так как АМ=МС, то ВМ=ВМ=МС.
Если медиана треугольника равна половине стороны, к которой она проведена, этот треугольник - прямоугольный.
Отсюда АС - диаметр описанной вокруг треугольника АВС окружности.
АС = 2r=14 см
По условию ВК=КС,
МК - медиана треугольника ВМС.
Так как ВМ - диаметр описанной вокруг треугольника ВМК окружности, - треугольник ВКМ прямоугольный.
Тогда КМ - высота треугольника ВМС, но она же и медиана.
Треугольник, в котором высота является медианой - равнобедренный.
Треугольник ВМС - равнобедренный.
ВМ=МС.
Так как АМ=МС, то ВМ=ВМ=МС.
Если медиана треугольника равна половине стороны, к которой она проведена, этот треугольник - прямоугольный.
Отсюда АС - диаметр описанной вокруг треугольника АВС окружности.
АС = 2r=14 см
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
11 лет назад
11 лет назад
11 лет назад