В треугольнике АВС угол В равен 120 градусов, а длина стороны АВ на 3*корень из 3 меньше полупериметра треугольника. Найдите радиус окружности, касающейся стороны ВС и продолжений сторон АВ и АС.
Ответы
Ответ дал:
0
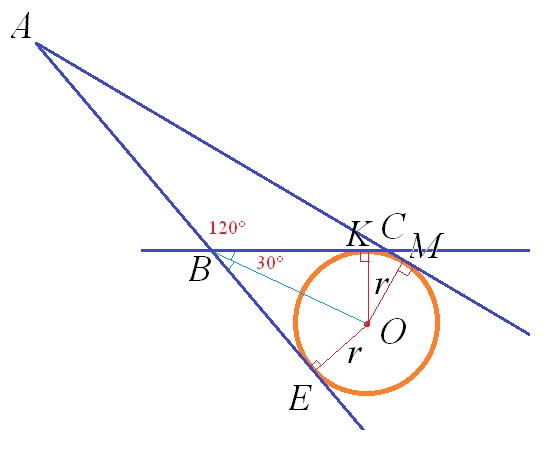
Чертеж к задаче во вложении.
Согласно условию

Пусть К, Е и М -точки касания окружности сторонами ∆АВС.
∠СВЕ=180°-∠АВС=180°-120°=60° (свойство смежных углов)
Т.к. О-центр окружности, то ВО - биссектриса ∠ЕВС. Значит, ∠СВО=∠ОВЕ=30°.
Обозначим радиус окружности OE=OK=OM=r.
В прямоугольном ∆ОЕВ

По свойству отрезков касательных ВЕ=ВК и СК=СМ, а также АЕ=АМ.
Отсюда P=АВ+ВС+АС = АВ+ВК+КС+АС=(АВ+ВЕ)+(АС+СМ)=АЕ+АМ=2АЕ. Значит,

Ответ: 3.
Согласно условию
Пусть К, Е и М -точки касания окружности сторонами ∆АВС.
∠СВЕ=180°-∠АВС=180°-120°=60° (свойство смежных углов)
Т.к. О-центр окружности, то ВО - биссектриса ∠ЕВС. Значит, ∠СВО=∠ОВЕ=30°.
Обозначим радиус окружности OE=OK=OM=r.
В прямоугольном ∆ОЕВ
По свойству отрезков касательных ВЕ=ВК и СК=СМ, а также АЕ=АМ.
Отсюда P=АВ+ВС+АС = АВ+ВК+КС+АС=(АВ+ВЕ)+(АС+СМ)=АЕ+АМ=2АЕ. Значит,
Ответ: 3.
Приложения:
Вас заинтересует
2 года назад
2 года назад
8 лет назад
8 лет назад
11 лет назад
11 лет назад