Question

Помогите, пожалуйста, очень прошу!))
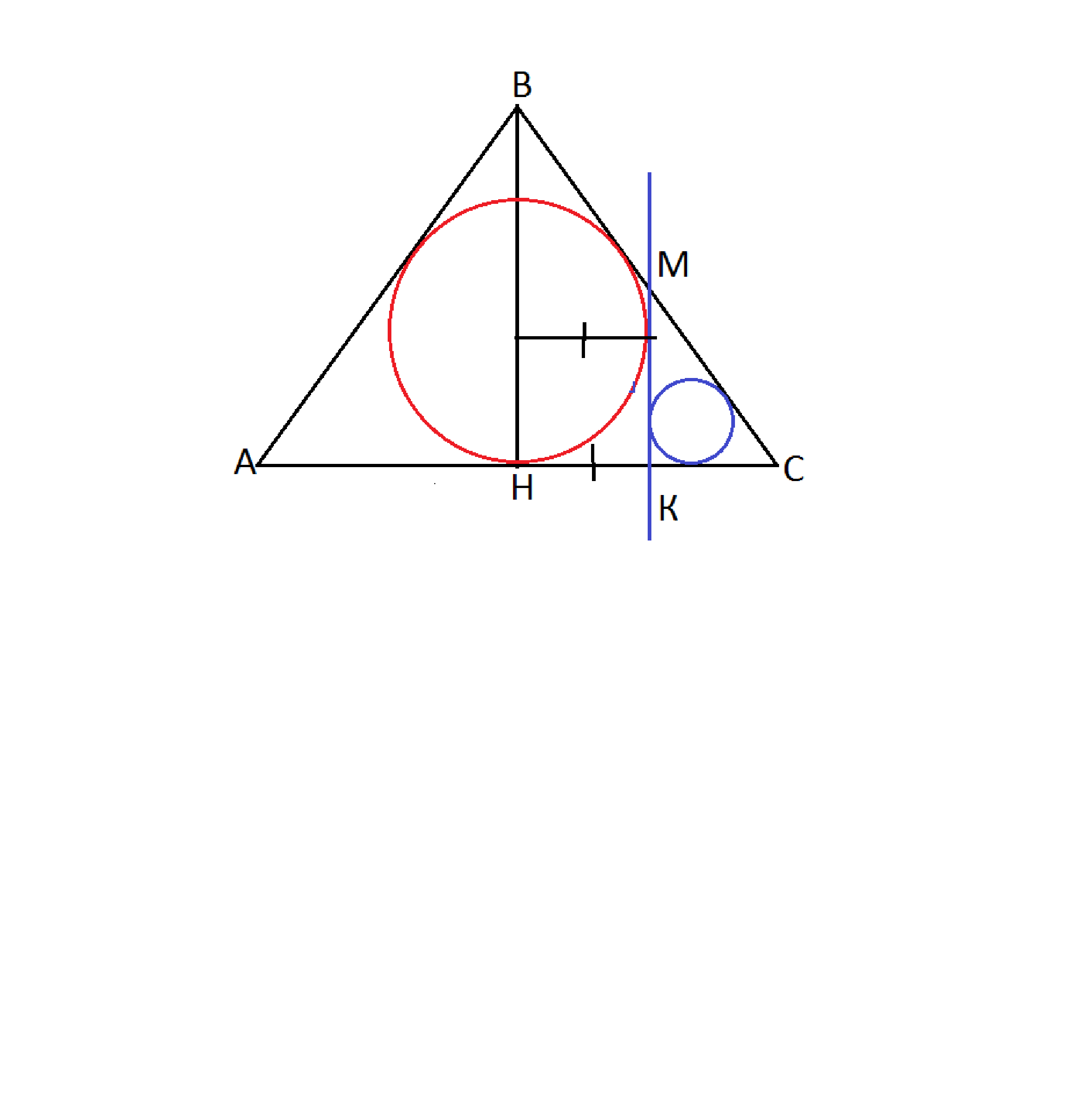
Боковая сторона равнобедренного треугольника 10, основание 12. К заданному основанию проведена высота. К окружности, писанной в этот треугольник, проведена касательная, параллельная построенной высоте и отсекающая от данного треугольника прямоугольный треугольник. Найти радиус окружности, вписанной в отсеченный треугольник.

Answer 1

Высота делит равнобедренный треугольник на два равных. 
Треугольник АВН - прямоугольный. 
АВ=10,
 АН=12:2=6 
Отсюда ВН= 8 ( треугольник египетский, соотношение сторон 3:4:5)
Радиус вписанной окружности можно найти по формуле :
r=S:p, где S- площадь, р - полупериметр. 
S=BH*AH=48
p=(2*10+12):2=16
r=48:16=3
НК=r=3
КС=НС-Н6-3=3
⊿МКС подобен⊿ВНС
Коэффициент подобия КС:НС=1/2
Стороны треугольника
МК=ВН:2=8:2=4 
МС=10:2=5 
S=4*3:2=6
 p=(4+3+5):2=6 
 r=S p=6:6=1
Или 
r=(а+b-с):2,  где КС=а, МК=b, МС=с
r=(3+4-5):2=1