в равнобедренной трапеции разноть двух углов равна 20 град. Найди наибольший угол этой трапеции. Ответ укажи в градусах.
Ответы
Ответ дал:
0
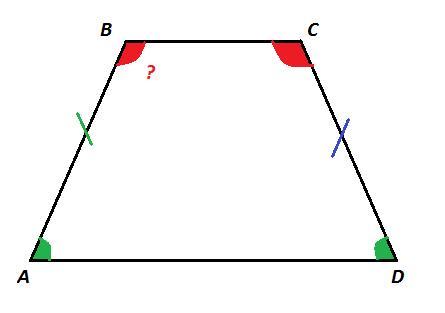
Равнобедренная трапеция ABCD, AB=CD, BC║AD
У равнобедренной трапеции углы при основаниях равны
∠A = ∠D; ∠B = ∠C
Тогда разность двух неравных углов ∠B-∠A=20° ⇔ ∠B=∠A+20°
Сумма углов при боковой стороне трапеции равна 180°
∠A + ∠B = 180°
∠A + ∠A + 20° = 180°
2∠A = 160° ⇒ ∠A = 80°
∠B = ∠A + 20° = 80° + 20° = 100°
Ответ: 100°
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад
9 лет назад
10 лет назад