Question

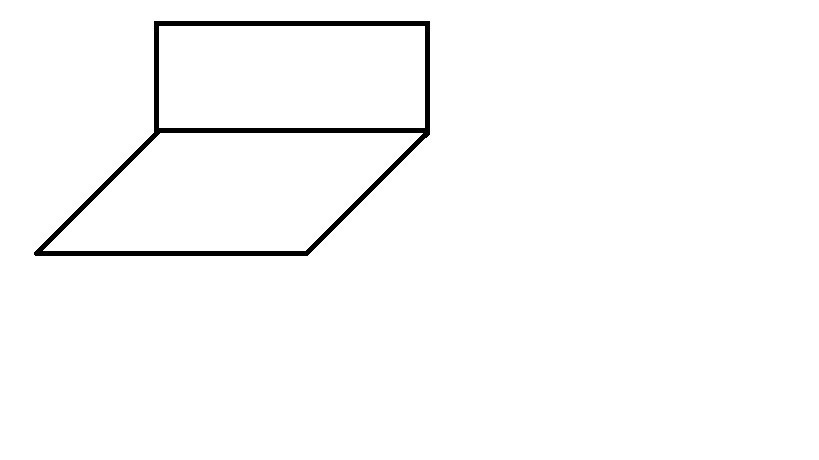
ABCD - квадрат с периметром 32, BMKC - прямоугольник с периметром 24. Плоскость ABCD и BMKC перпендикулярны. Найдите MD.

P.S. Тот что похож на параллелограмм обозначается ABCD. BC - общая сторона

Answer 1

P(ABCD)=32 т.к. это квадрат, то у него все стороны равны
P(ABCD)=a+a+a+a
32=4a
a=8

BC=a=8
(ABC)∩(BMK)=BC , поэтому BC ∈ (BMK) и BC ∈ (ABC)

P(BMKC)=24
P(BMKC)=a+a+b+b
24=8+8+2b
2b=8
b=4
MB=b=4

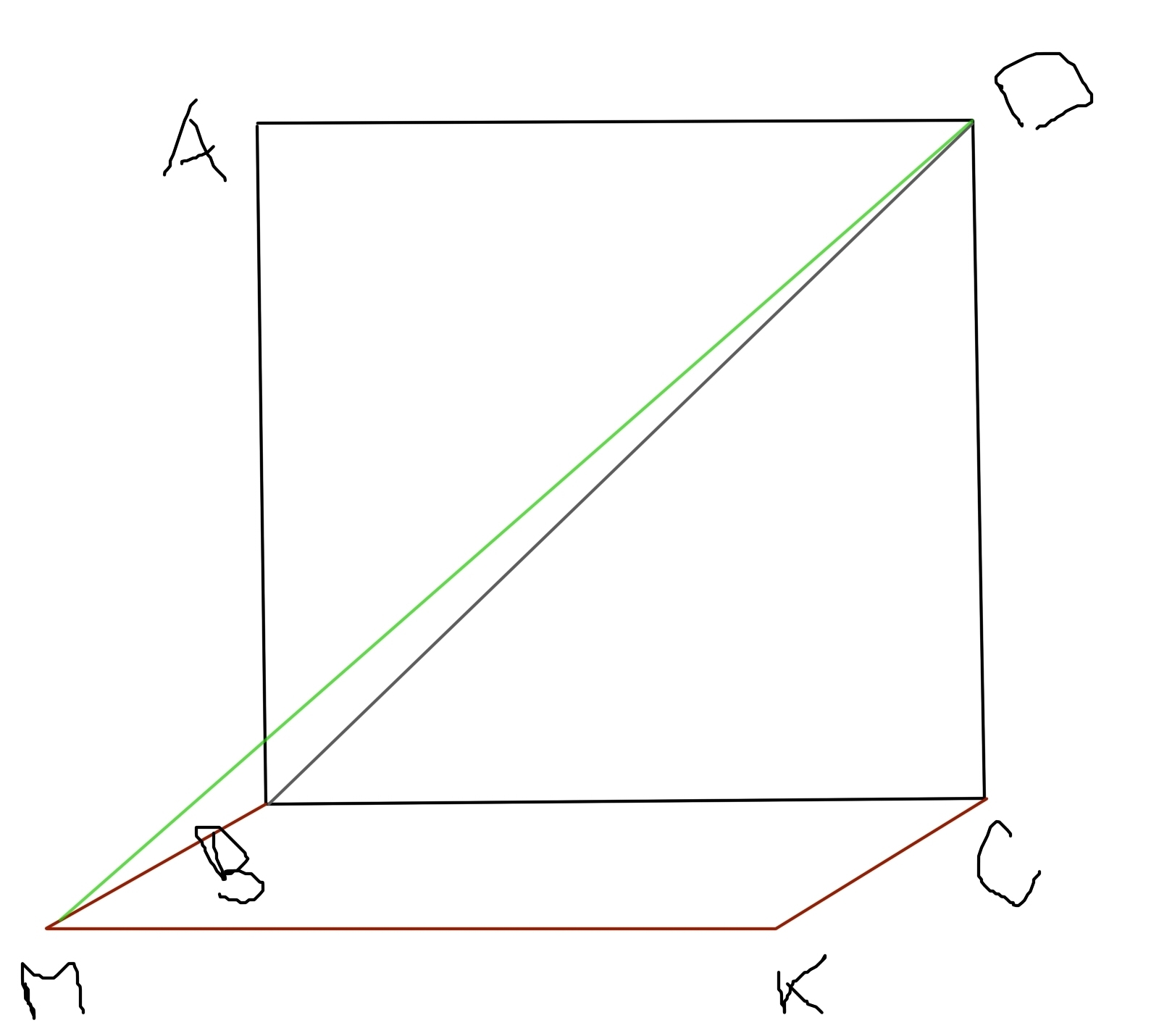
В ΔBCD - прямоуг. т.к. ABCD - квадрат
По т.П. $BD^{2} = BC^{2} + DC^{2}$
$BC^{2} = sqrt{64 + 64} = sqrt{128}$

В ΔMBD - прямоуг. MB⊥BD (MB⊥BD т.к. лежат в перпендикулярных пл.)
по Т.П. $MD^{2} = BD^{2} + MB^{2}$
$MD = sqrt{128 + 16} = sqrt{144} =12$
Ответ: 12