Question

Хорда окружности равна 10 см. Через один конец хорды проведена касательная к окружности, а через другой — секущая, параллельная касательной. Определить радиус окружности, если внутренний отрезок секущей равен 12 см.

Answer 1

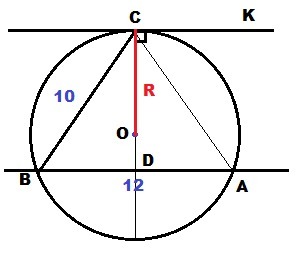
Дано: окружность с центром в точке О.
ВС = 10 см - хорда.  СК - касательная. 
АВ║СК,  АВ = 12 см
Найти: R

ОС⊥СК   -   радиус в точку касания
АВ║СК  ⇒   CD⊥АВ    ⇒
AD = DB  -   радиус, перпендикулярный хорде, делит ее пополам ⇒
CD - высота и медиана в ΔABC   ⇒
ΔABC - равнобедренный : AC = BC = 10
Площадь ΔABC по формуле Герона
$p = frac{AB+BC+AC}{2} = frac{12+10+10}{2} =16 \ \ S_{ABC}= sqrt{p(p-AB)(p-BC)(p-AC)} = \ \ = sqrt{16(16-12)(16-10)(16-10)} = \ \ = sqrt{16*4*6*6} =4*2*6=48$
Площадь ΔABC через радиус описанной окружности
$S_{ABC}= frac{AB*AC*BC}{4R} \ \ R= frac{AB*AC*BC}{4S_{ABC}} = frac{12*10*10}{4*48} = frac{25}{4} =6,25$

Радиус окружности  R = 6,25