Question

сторона основания правильной четырехугольной пирамиды равна a , а ее диагональное сечение - прямоугольный треугольник. найдите объем пирамиды
с рисунком, если можно)

Answer 1

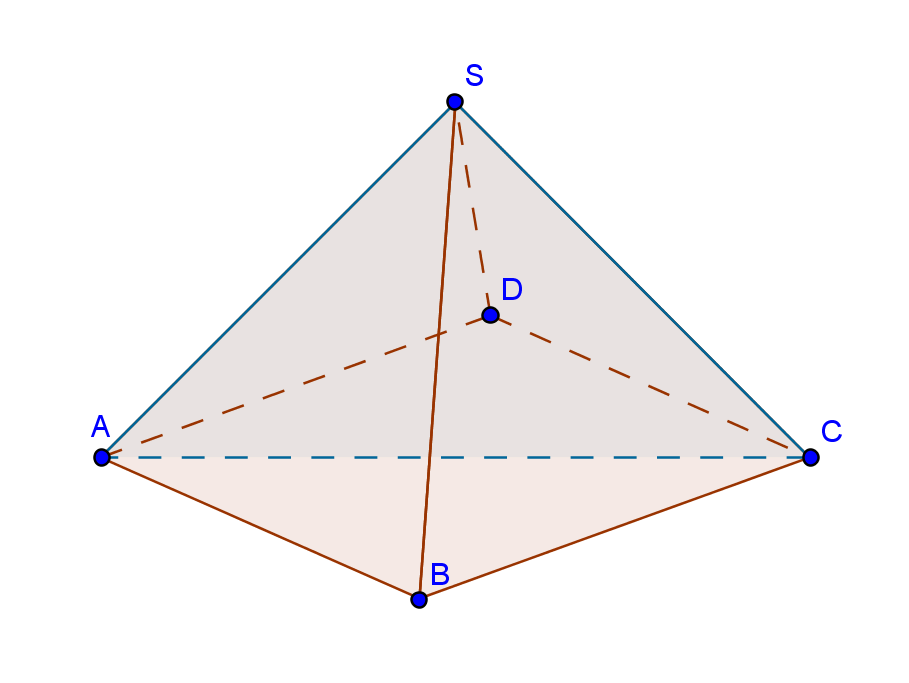
Пирамида правильная, поэтому боковые ребра равны и треугольник ASC равнобедренный (и прямоугольный). Гипотенуза AС является диагональю основания - квадрата ABCD. Её длину несложно найти: AC = a*sqrt(2).
Длину бокового ребра AS можно найти, например, так: AS = AC * sin(45) = a.

Найдем высоту пирамиды, одновременно являющуюся высотой треугольника ASC, опущенной на основание AC. Написав выражения для треугольника ASC двумя способами, получаем h = AS * SC / AC = a^2 / (a sqrt(2)) = a sqrt(2)/2

V = 1/3 Sосн h = 1/3 a^2 a sqrt(2)/2 = a^3 sqrt(2) / 6