ПОМОГИТЕ С ЛОГАРИФМАМИ
Желательно бы решить первый и второй
Очень надеюсь на вашу помощь:(
Приложения:
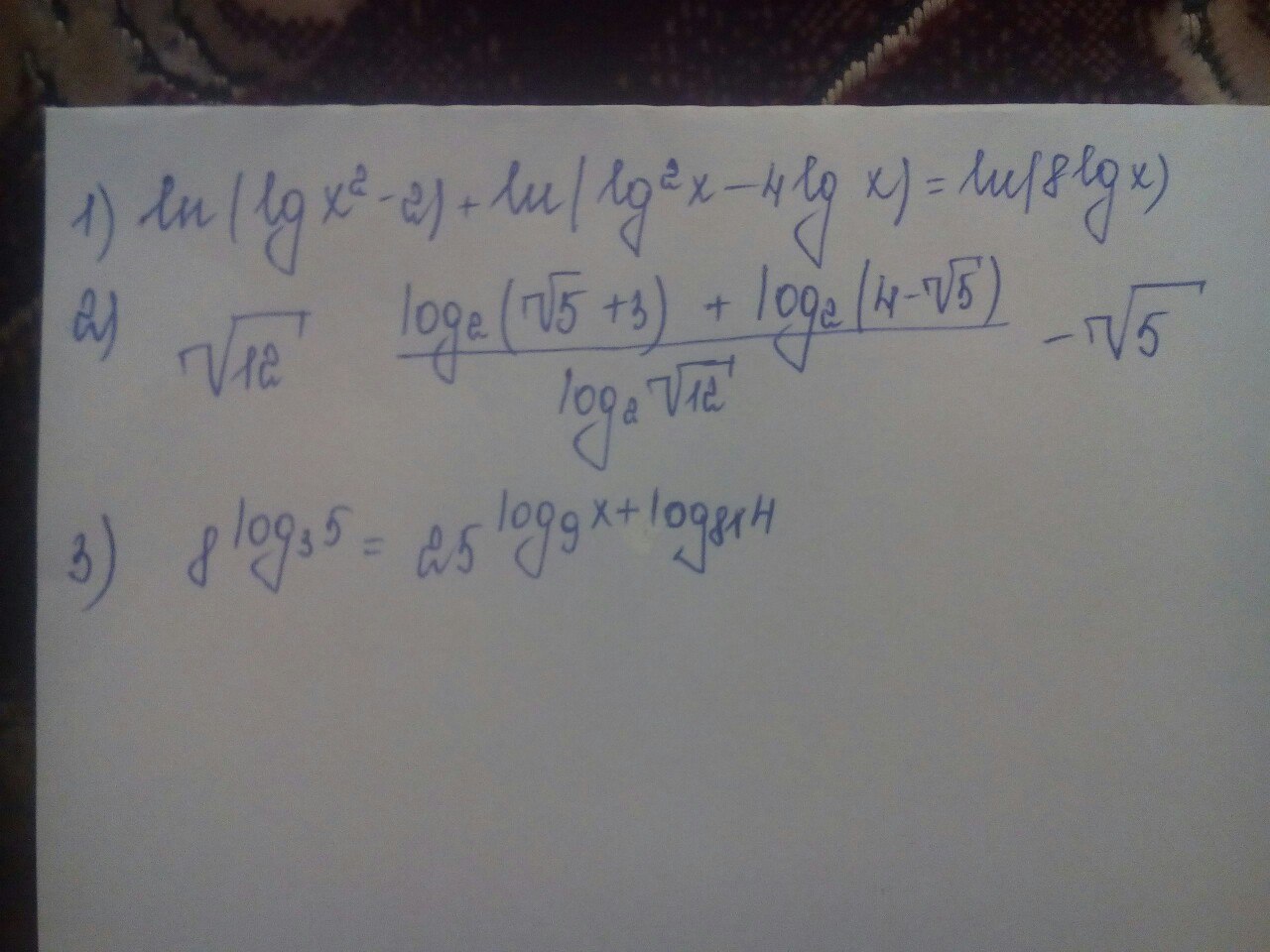
Ответы
Ответ дал:
0
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад