Ответы
Ответ дал:
0
Возводим в квадрат, сразу частично приведя подобные. Произведения двух корней в левой и правой части равны, сумма квадратов слагаемых слева на 9 + 1 + 16 - 4 - 4 = 18 больше, чем справа:
Подставляем получившееся в исходное уравнение, и там остаётся только:
Единственный кандидат на то, чтобы быть корнем, это x = 0. Подстановка x = 0 в уравнение приводит к верному равенству, значит, x = 0 - корень.
Ответ. x = 0.
Ответ дал:
0
Решение прицеплено в картинке
Приложения:
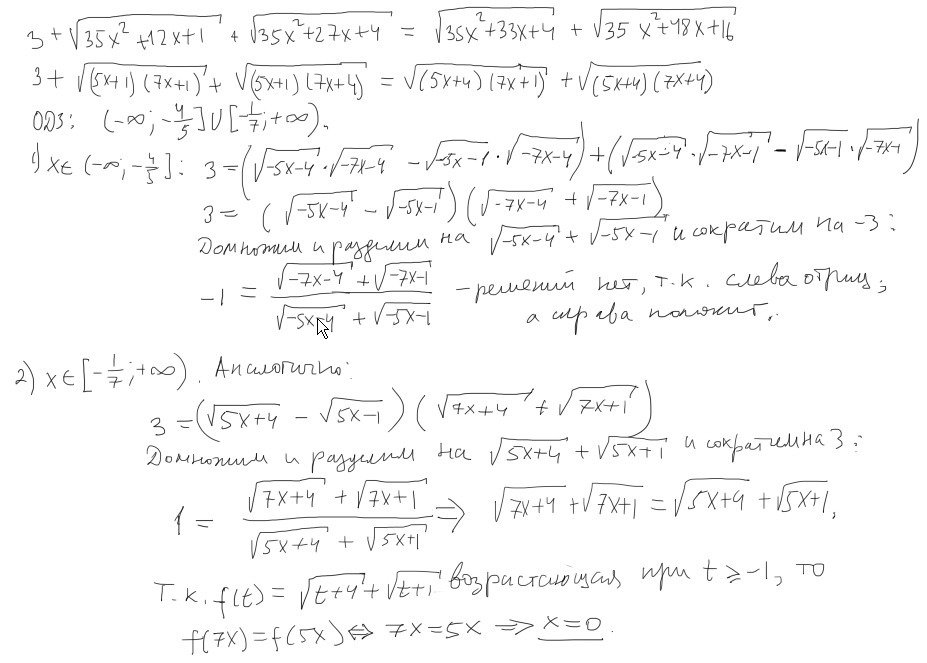
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад