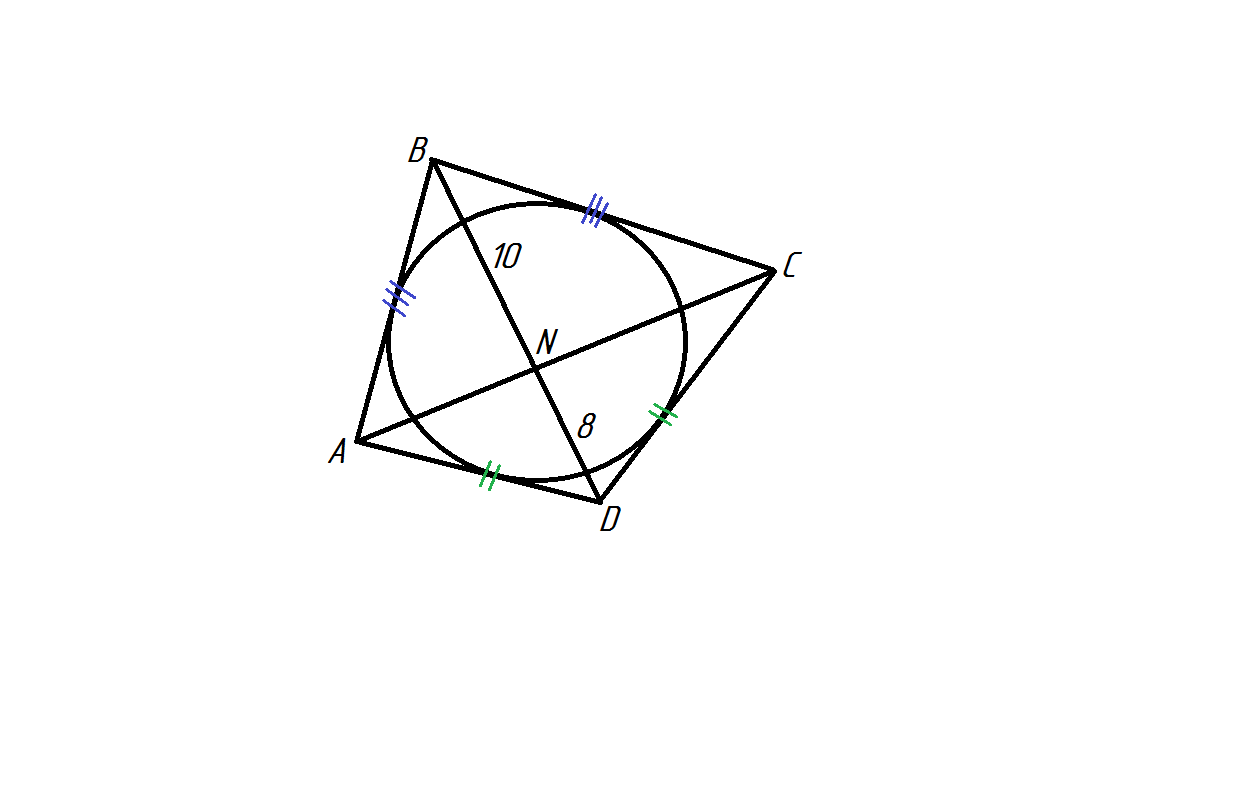
B четырёхугольник ABCD вписана окружность, N - точка пересечения диагоналей AC и BD . Известно что AD=DC, BN=10,ND=8. Найти AD
Ответы
Ответ дал:
0
Воспользуемся следующей теоремой:
В выпуклый четырехугольник можно вписать окружность, только в том случае, если суммы противоположных сторон равны, получаем:

Так как соседние стороны попарно равны, то получаем что эта фигура квадрат, в ином случае такое соотношение не сохраняется.
Получаем что сторона будет равна:

Рисунок во вложении
В выпуклый четырехугольник можно вписать окружность, только в том случае, если суммы противоположных сторон равны, получаем:
Так как соседние стороны попарно равны, то получаем что эта фигура квадрат, в ином случае такое соотношение не сохраняется.
Получаем что сторона будет равна:
Рисунок во вложении
Приложения:
Вас заинтересует
2 года назад
8 лет назад
8 лет назад
10 лет назад
11 лет назад