Question

Угол между биссектрисой и высотой, проведенными из вершины прямого угла прямоугольного треугольника равен 12 градусов.Найдите острые углы треугольника.

Answer 1

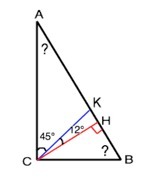
Обозначим в ∆ АВС биссектрису СК, высоту СН. 

Биссектриса прямого угла делит его на два равных по 45°. 

Высота  от угла КСВ, равного 45°, "отсекает" 12°, и

∠НСВ=45°-12°=33°

Сумма острых углов прямоугольного треугольника равна 90°.

∠АВС=90°-НСВ=90°-33°=57°

∠САВ=НСВ=90°-57°=33°