Здравствуйте, помогите решить домашнее задание по теме:
«Производная и её применение . Первообразная.»
Найдите промежутки возрастания и убывания функции:
Приложения:
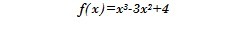
Ответы
Ответ дал:
0
f(x) = x³-3x²+4
f'(x)= (x³-3x²+4)' = 3x²-6x
найдем точки, в которых f'(x) = 0
3x²-6x = 0
3х(х-2)=0
3х=0 или х-2=0
х=0 или х=2
___+___0____-___2_____+____
f(x) возрастает при х∈(-∞;0)∪(2; +∞)
f(х) убывает при х∈(0;2)
f'(x)= (x³-3x²+4)' = 3x²-6x
найдем точки, в которых f'(x) = 0
3x²-6x = 0
3х(х-2)=0
3х=0 или х-2=0
х=0 или х=2
___+___0____-___2_____+____
f(x) возрастает при х∈(-∞;0)∪(2; +∞)
f(х) убывает при х∈(0;2)
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад