Question

найдите площадь ромба сторона которого равна 17 см, а разница диагоналей 14 см, Заранее спасибо!

Answer 1

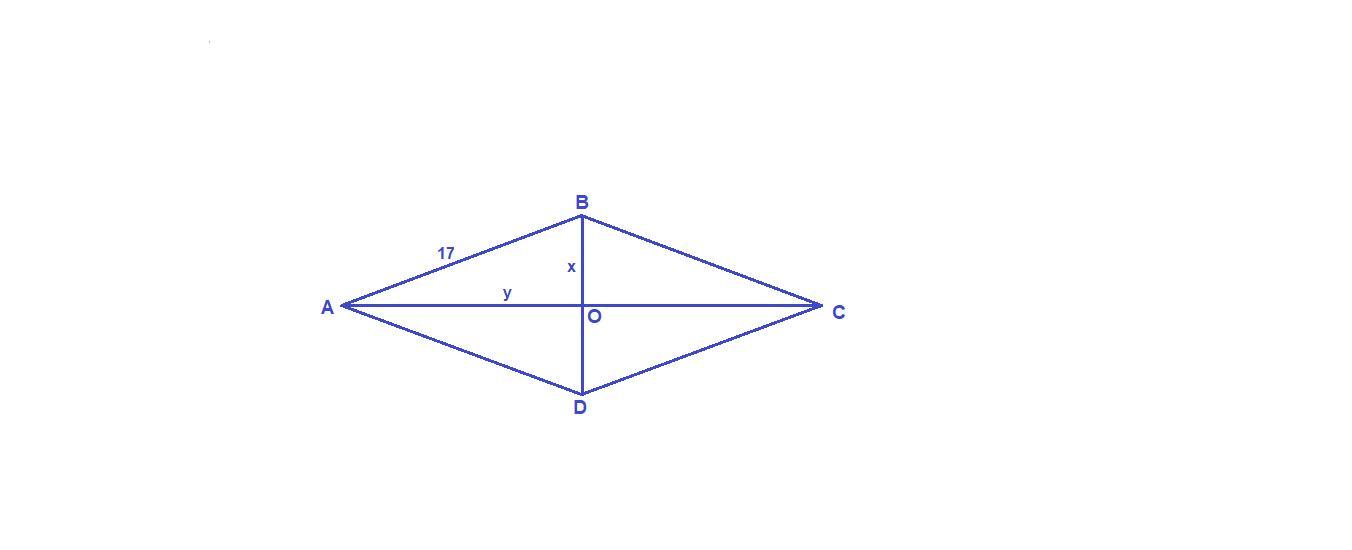
Стороны ромба равны, диагонали перпендикулярны и точкой пересечения делятся пополам.

Обозначим половины диагоналей х и у.

Если 2у - 2х = 14, то у - х = 7.

Из прямоугольного треугольника АОВ по теореме Пифагора:

АВ² = АО² + ВО²

Получаем систему уравнений:

y - x = 7

y² + x² = 289

Возведем обе части первого уравнения в квадрат:

y² + x² - 2xy = 49

Подставим значение суммы квадратов из второго уравнения:

289 - 2xy = 49

2xy = 289 - 49

2xy = 240

Sabcd = 1/2 · AC · BD = 1/2 · 2x · 2y = 2xy

Sabcd = 240 см²