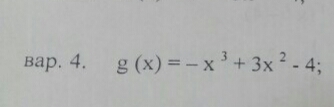Ответы
Ответ дал:
0
ДАНО
g(x) = - x³ + 3x² - 4
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. g(x)=0
при х1 = -1 и х2,3 = 2.
3. Пересечение с осью У. g(0) = - 4.
4. Поведение на бесконечности.lim g(-∞) = - ∞ lim g(+∞) = +∞
5. Исследование на чётность.g(-x) = x³ + 3x² -4 ≠ g(x).
Функция ни чётная ни нечётная.
6. Производная функции.g'(x)= -3*x² + 6x
7. Корни: при Х=0 g(0) = -4 - минимум
при Х=2 - g(2) = 0 - максимум
Возрастает - Х∈[0;2]
Убывает - X∈(-∞;0]∪[2;+∞)
8. Вторая производнаяY"(x) = -6x + 6
9. Точка перегиба g"(x)=0 при X=1.
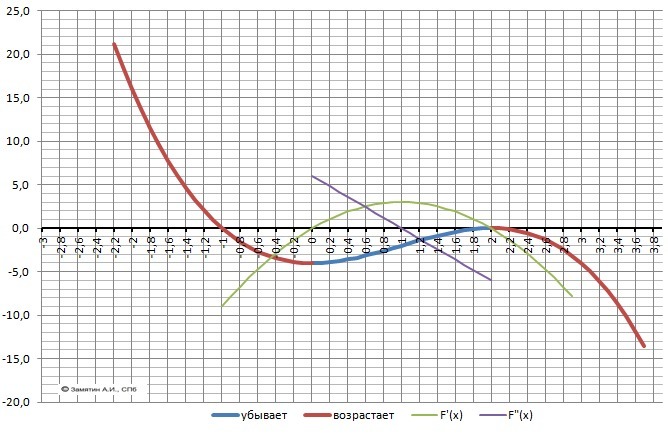
10. График в приложении.
g(x) = - x³ + 3x² - 4
ИССЛЕДОВАНИЕ
1. Область определения - Х∈(-∞;+∞) - непрерывная.
2. Пересечение с осью Х. g(x)=0
при х1 = -1 и х2,3 = 2.
3. Пересечение с осью У. g(0) = - 4.
4. Поведение на бесконечности.lim g(-∞) = - ∞ lim g(+∞) = +∞
5. Исследование на чётность.g(-x) = x³ + 3x² -4 ≠ g(x).
Функция ни чётная ни нечётная.
6. Производная функции.g'(x)= -3*x² + 6x
7. Корни: при Х=0 g(0) = -4 - минимум
при Х=2 - g(2) = 0 - максимум
Возрастает - Х∈[0;2]
Убывает - X∈(-∞;0]∪[2;+∞)
8. Вторая производнаяY"(x) = -6x + 6
9. Точка перегиба g"(x)=0 при X=1.
10. График в приложении.
Приложения:
Вас заинтересует
2 года назад
2 года назад
9 лет назад