Question

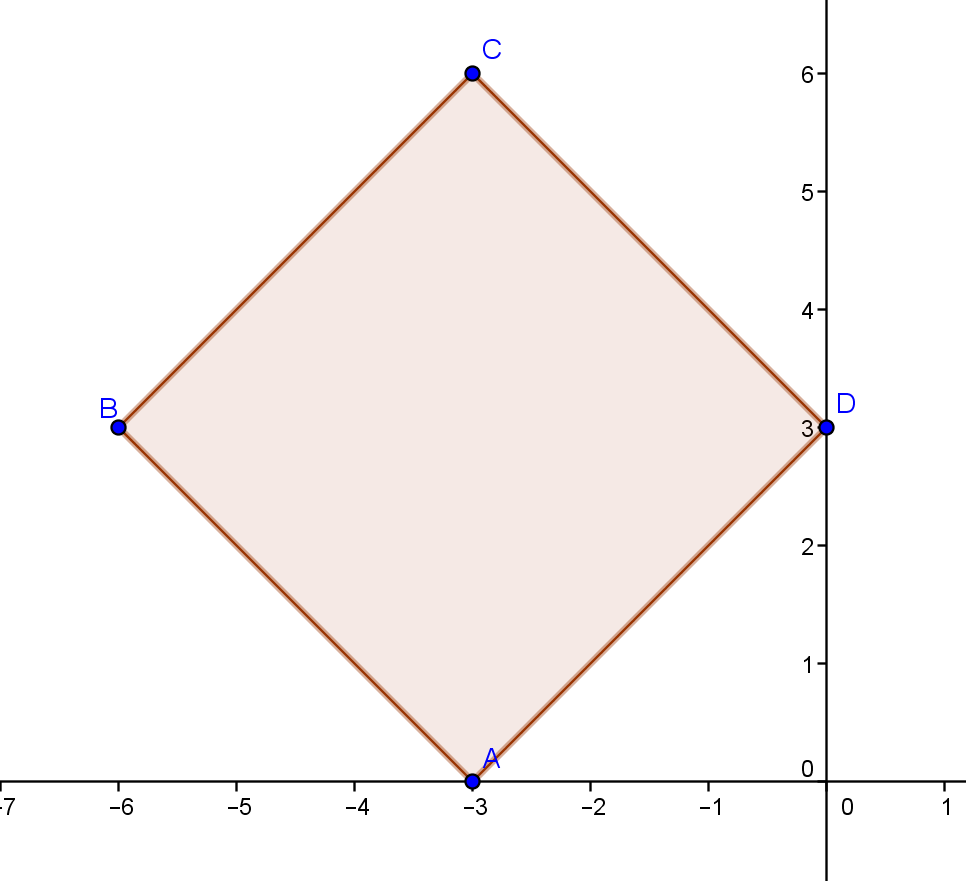
Найдитк площадь квадрата,вершины которого заданы координатами в декартовой системе координат А(-3;0).В(-6;3).С(-3;6).D(0;3).

Answer 1

Это последовательные вершины квадрата.Найдём расстояние между вершинами, оно будет равно длине стороны квадрата.
 $AB=sqrt{(-6+3)^2+(3-0)^2}=sqrt{9+9}=3sqrt{2}\BC=sqrt{(-3+6)^2+(6-3)^2}=sqrt{9+9}=3sqrt{2}\CD=sqrt{(0+3)^2+(3-6)^2}=sqrt{9+9}=3sqrt{2}\AD=sqrt{0+3)^2+(3-0)^2}=3sqrt{2}\S=3sqrt{2}cdot 3sqrt{2}=9cdot 2=18$

Answer 2

Найдены длины всех сторон, чтобы убедиться, что перед нами действительно квадрат.

Answer 3

Недоверчивость - это хорошо) Но вы доказали, что это ромб. Для квадрата нужна еще перпендикулярность сторон.

Answer 4

Да, согласна.

Answer 5

Для того, чтобы найти площадь квадрата, нужно возвести в квадрат длину его стороны.
Найдем сторону, для этого обратимся к рисунку. По рисунку проще всего найти длину стороны AD. Для этого напишем выражение по теореме Пифагора:
AD^2 = 3^2 + 3^2 = 18
Можно было бы найти непосредственно длину отрезка AD, но лучше сразу заметить, что мы нашли как раз то, что искали - сторону в квадрате! Поэтому сразу пишем ответ
S = 18