Question

Докажите теорему о том, что если две параллельные прямые пересечены секущей, то накрест лежащие углы равны. Напишите нормальное доказательство!

Answer 1

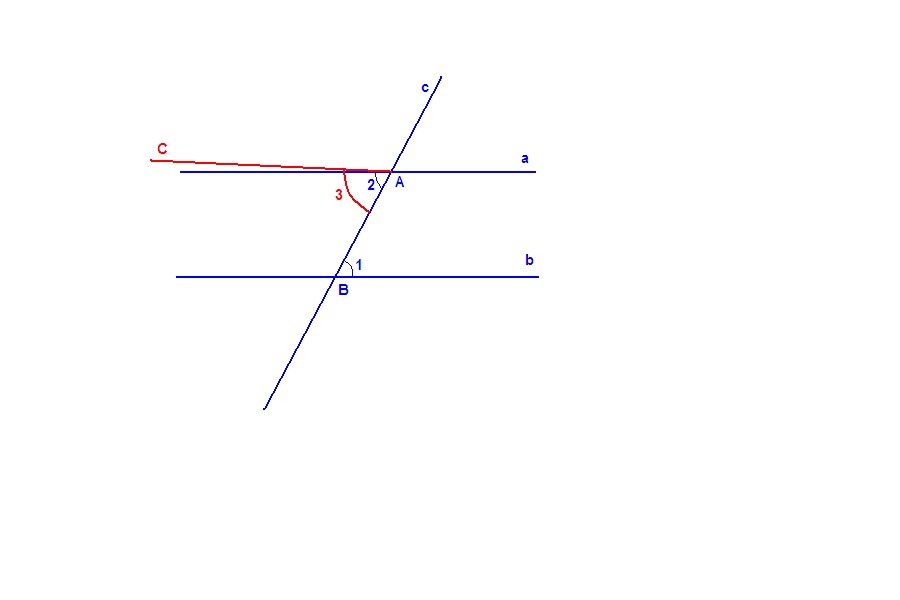
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.

Дано: а║b, с - секущая.

Доказать: ∠1 = ∠2.

Доказательство.

Предположим, что ∠1 ≠ ∠2. От луча АВ отложим угол 3, равный углу 1. Тогда прямая АС параллельна прямой b (внутренние накрест лежащие углы 1 и 3 равны). Но тогда через точку А проходит две прямые, параллельные прямой b. Предположение неверно. Значит ∠1 = ∠2.