Question

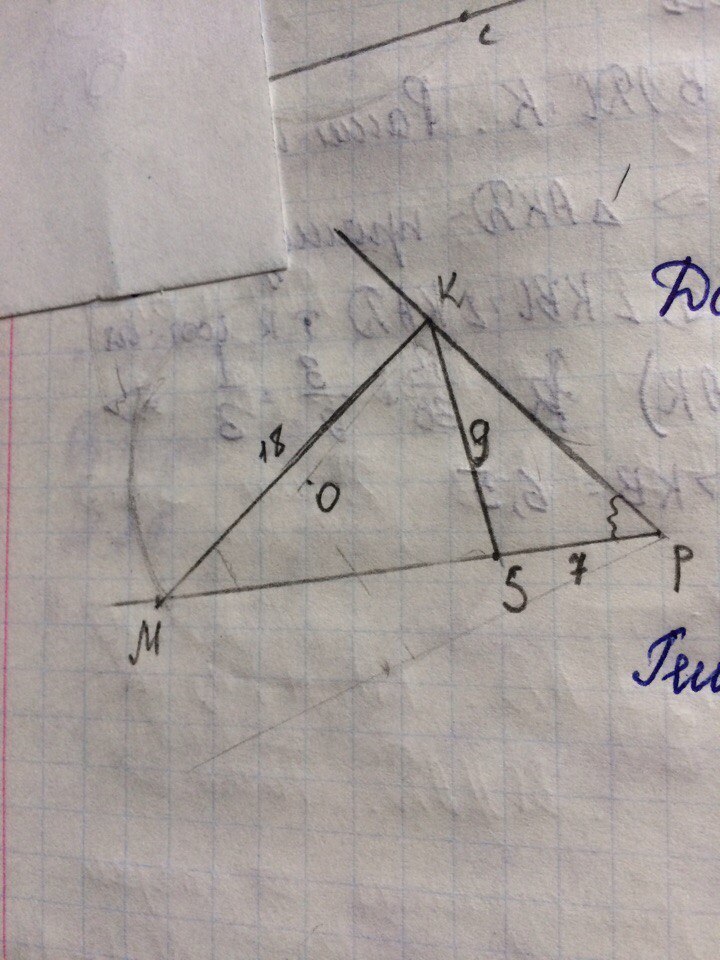
Дан треугольник MKP. Окружность с центром в точке О касается стороны PK в точке К и пересекает сторону MP в точке S. KM=18, KS=9, SP=7. Найти MS.
MK не является диаметром.

Answer 1

Для данной окружности КР - касательная и МР - секущая.

По теореме о касательной и секущей КР²=PS·MP, отсюда КР/PS=МР/КР. С таким отношением сторон и общим углом Р треугольники KSP и МКР подобны. Для них можно записать следующую пропорцию:
PS/KS=КР/МК ⇒ КР=PS·MK/KS=7·18/9=14.
Также КР/PS=МР/КР ⇒ МР=КР²/PS=14²/7=28.

Итак, МS=MP-PS=28-7=21 - это ответ.

Answer 2

Спасибо большое