В остроугольном треугольнике ABC высота АН равна 9 корней из 69,а сторона АВ равна 75. Найдите cos B
Ответы
Ответ дал:
0
Дано:
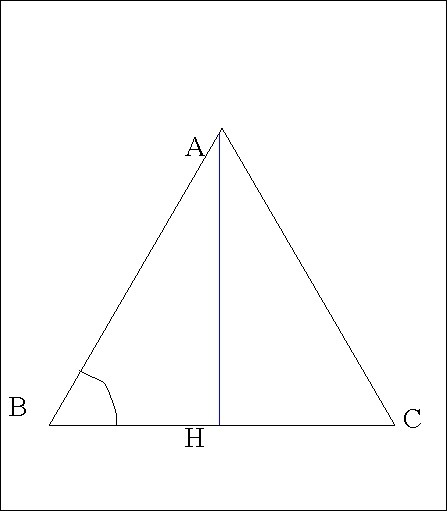
ΔАВС
АН⊥ВС
АН = 9√69
АВ = 75
Найти cos∠B
Косинус угла - это отношение прилежащего катета к гипотенузе.
cos∠B = BH/AB
По теореме Пифагора из прямоугольного ΔАВН найдём ВН.
ВН² = АВ² - АН²
ВН² = 75² - (9√69)² = 5625 - 5589 = 36
ВН = √36 = 6
ВН = 6
А теперь найдём cos∠B.
cos∠B = BH/AB
cos∠B = 6/75= 0,08
Ответ: cos∠B = 0,08.
ΔАВС
АН⊥ВС
АН = 9√69
АВ = 75
Найти cos∠B
Косинус угла - это отношение прилежащего катета к гипотенузе.
cos∠B = BH/AB
По теореме Пифагора из прямоугольного ΔАВН найдём ВН.
ВН² = АВ² - АН²
ВН² = 75² - (9√69)² = 5625 - 5589 = 36
ВН = √36 = 6
ВН = 6
А теперь найдём cos∠B.
cos∠B = BH/AB
cos∠B = 6/75= 0,08
Ответ: cos∠B = 0,08.
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
10 лет назад