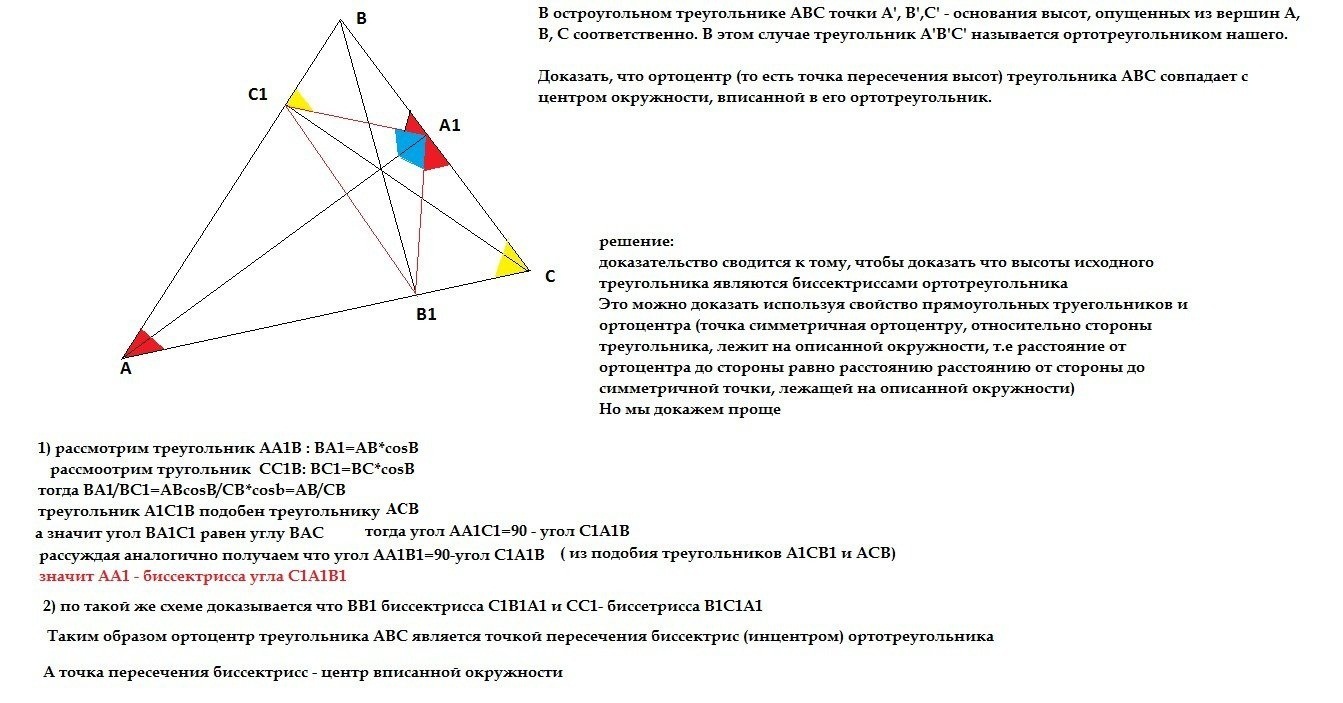
В остроугольном треугольнике ABC точки A', B',C' - основания высот, опущенных из вершин A, B, C соответственно. В этом случае треугольник A'B'C' называется ортотреугольником нашего.
Доказать, что ортоцентр (то есть точка пересечения высот) треугольника ABC совпадает с центром окружности, вписанной в его ортотреугольник.
Ответы
Ответ дал:
0
В остроугольном треугольнике ABC точки A', B',C' - основания высот, опущенных из вершин A, B, C соответственно. В этом случае треугольник A'B'C' называется ортотреугольником нашего.
Доказать, что ортоцентр (то есть точка пересечения высот) треугольника ABC совпадает с центром окружности, вписанной в его ортотреугольник.
Решение в приложении
Доказать, что ортоцентр (то есть точка пересечения высот) треугольника ABC совпадает с центром окружности, вписанной в его ортотреугольник.
Решение в приложении
Приложения:
Вас заинтересует
2 года назад
2 года назад
7 лет назад
7 лет назад
9 лет назад
9 лет назад
10 лет назад