Question

в равнобедренном треугольнике abc с основанием ac проведена медиана BM на ней взята точка D Докажите равенство треугольников ABO CBO

Answer 1

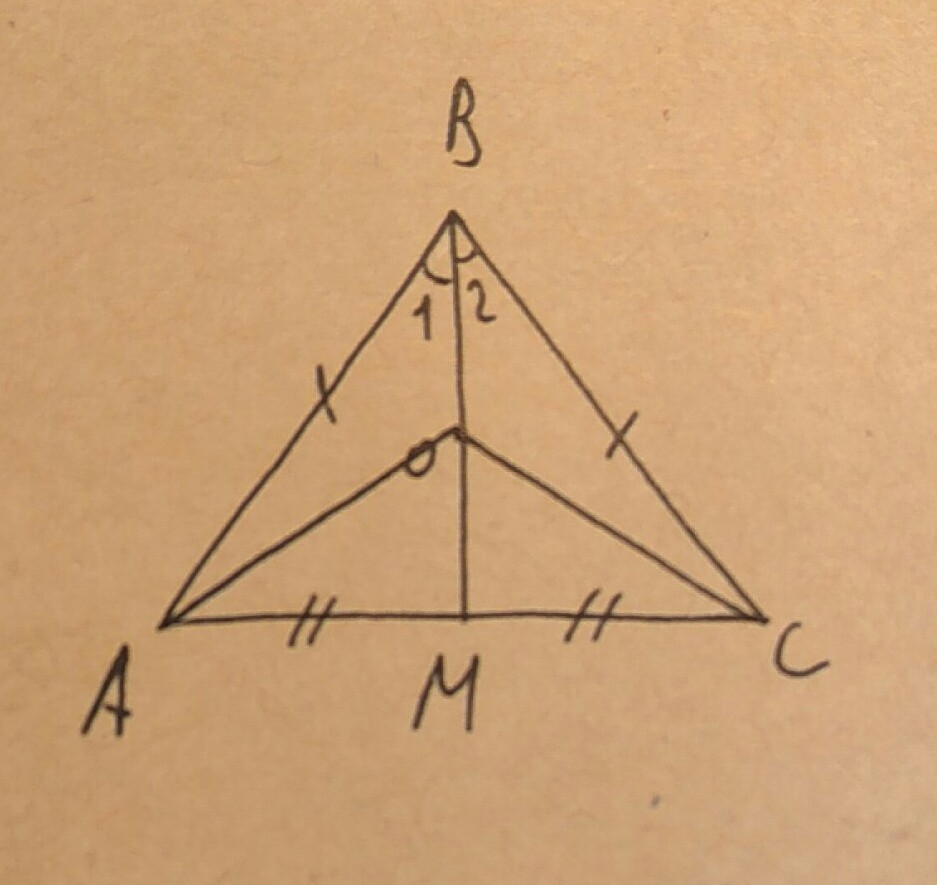
Дано: ABC - равнобедренный ∆-к;
AB=BC;
BM - медиана;
точка O принадлежит BM.
Доказать, что ABO = CBO
Доказательство:
1.AB=BC (по условию)
2.BO — общая.
треугольник равнобедренный → BM — биссектриса
3. угол 1 = углу 2 (по свойству биссектрисы)
т. о. ∆-к ABO = ∆-ку CBO (по двум сторонам и углу между ними)

Answer 2

а напиши что в решение писать

Answer 3

то, что после слова "доказательство" — это и есть решение

Answer 4

а что тогда доказательство

Answer 5

точнее что туда писать

Answer 6

если в задаче написано доказать что-то, то задача строится по схеме "дано - доказать - доказательство". грубо говоря, доказательство - это решение задачи.