Question

Радиусы двух пересекающихся окружностей равны 17 см и 39 см, а расстояние
между их центрами – 44 см. Найдите длину общей хорды окружностей.

Answer 1

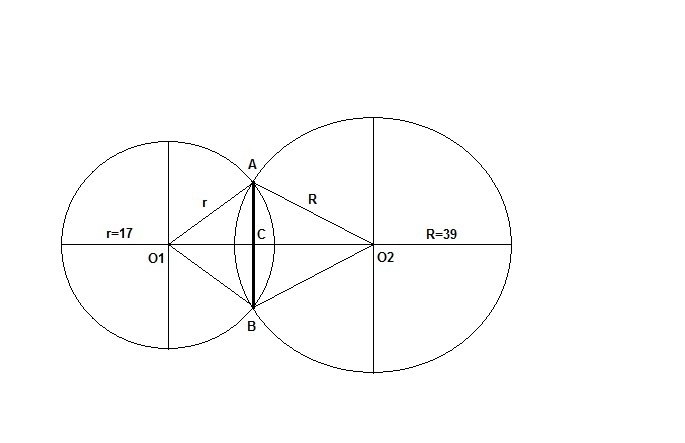
Вот рисунок. Расстояние между центрами O1O2 = 44 см.
Расстояния от центра окружности до хорды O1C = x см, O2C = 44-x см.
Длина хорды AB = a см; AC = BC = a/2 см.
По теореме Пифагора
{ x^2 + (a/2)^2 = r^2
{ (44 - x)^2 + (a/2)^2 = R^2
Подставляем известные величины
{ x^2 + a^2/4 = 17^2 = 289
{ 44^2 - 88x + x^2 + a^2/4 = 39^2 = 1521
Подставляем 1 уравнение во 2 уравнение
1936 - 88x + 289 = 1521
x = (1936 + 289 - 1521)/88 = 704/88 = 8
Подставляем это в 1 уравнение
8^2 + a^2/4 = 289
a^2 = (289 - 64)*4 = 225*4 = 900
a = AB = 30 см

Answer 2

Короче та дорога, которую знаешь.

Answer 3

Как доказать что O1CA, O1CB, O2AC,O2BC прямоугольные?

Answer 4

Это следует из того, что касательная к окружности перпендикулярна радиусу.

Answer 5

Если окружности разъедутся в разные стороны, и станут касательными, то общая касательная к ним будет перпендикулярна обоим радиусам. Поэтому общая хордатоже перпендикулярна обоим радиусам.

Answer 6

Спасибо, все объяснили просто и понятно