Прямоугольный треугольник MKL вписан в окружность радиусом 13 см. Найдите длину высоты MH, опущенной на наибольшую сторону треугольника, если HL=8 см.
Помогите плиз начертить рисунок к этому задачу а то я совсем запуталась
Ответы
Ответ дал:
0
Пояснение к чертежу:
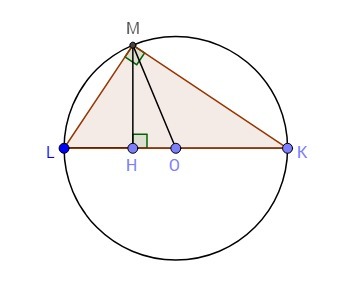
Наибольшая сторона прямоугольного треугольника - гипотенуза, значит ∠М=90°; LK - гипотенуза. Точка О - центр описанной окружности (лежит на середине гипотенузы).
Решение:
LK = 13*2 = 26 cм (диаметр)
НК = LK-LH = 26 - 8 = 18 cм
НО = LO-LH = 13-8 = 5 cм
ОМ = 13 см (радиус)
Из ΔМНО найдем катет МН по т.Пифагора:
МН= √(13²-5²) = √144 = 12 см
Ответ: 12 см.
Наибольшая сторона прямоугольного треугольника - гипотенуза, значит ∠М=90°; LK - гипотенуза. Точка О - центр описанной окружности (лежит на середине гипотенузы).
Решение:
LK = 13*2 = 26 cм (диаметр)
НК = LK-LH = 26 - 8 = 18 cм
НО = LO-LH = 13-8 = 5 cм
ОМ = 13 см (радиус)
Из ΔМНО найдем катет МН по т.Пифагора:
МН= √(13²-5²) = √144 = 12 см
Ответ: 12 см.
Приложения:
Ответ дал:
0
спасибо
Вас заинтересует
7 лет назад
10 лет назад